Zeiger – Herr Fessa

Fourier-Reihen, Teil 7 – wie Signale in Frequenzen zerlegt werden

Wenn wir ein Signal in eine Fourier-Reihe »entwickeln«, müssen wir herausfinden, welche Frequenzen in diesem Signal stecken. Die Formeln dazu haben wir schon in Teil 3 gesehen. Aber warum funktioniert das – speziell bei gemessenen Signalen – wirklich?

Fourier-Reihen, Teil 6b – DFT gemessener Signale

Im letzten Teil haben wir die Fourier-Koeffizienten eines Signals s numerisch berechnet, unter der Voraussetzung, die Periodendauer des Signals zu kennen.

Wenn wir ein Signal messen, kennen wir dessen Periodendauer normalerweise nicht. Wir messen einfach während der Messdauer $T_m$ mit der Sampling-Frequenz (Abtastrate) $f_s$ die momentanen Werte $s(t)$ . Wie beeinflusst das die Fourier-Koeffizienten?

Abb. 1 zeigt nochmals unser Signal

$s(t) = -1 + 3\sin(2\pi \cdot 0.5\,\text{Hz} \cdot t + \pi) + 2\sin(5 \cdot 2\pi \cdot 0.5\,\text{Hz} \cdot t - \tfrac{\pi}{2})$

aus dem letzten Teil.

sampled_meas_sig — Abb. 1: Das Signal aus Teil 6. Innerhalb der Messdauer von 3.5 s ist das Signal dicker gezeichnet. Der hellblaue Verlauf ist die tatsächliche Periodizität, der hellrote Verlauf die scheinbare Periodizität. Die roten Punkte sind die 32 Messwerte.

Zeiger und Wechselspannungen bzw. Wechselströme

(2023-11-03: Videos zur Motivation komplexer Zahlen mit Wechselströmen gibt es hier auf Deutsch und hier auf Englisch.)

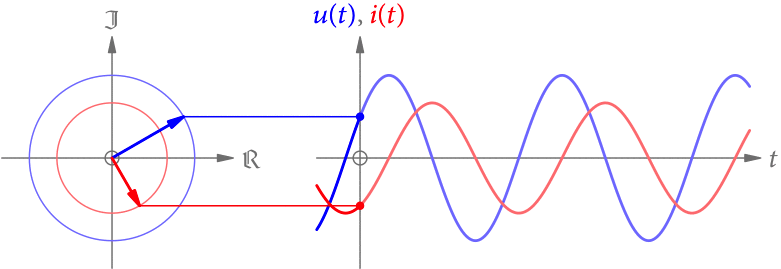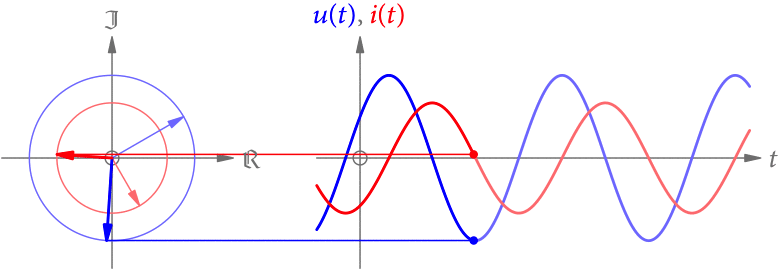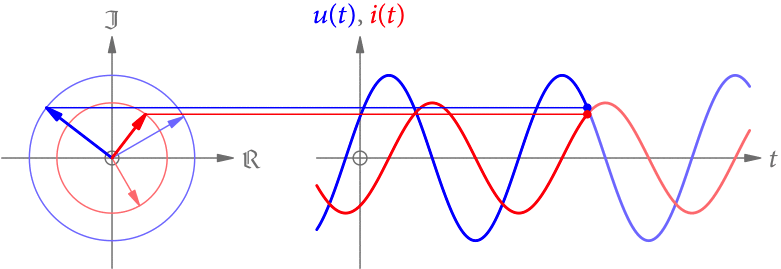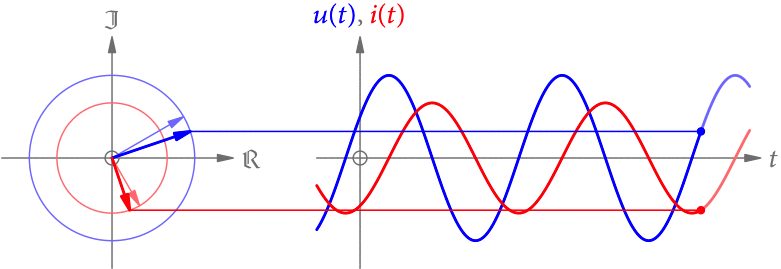
(2018-05-21 überarbeitet) Wechselspannungen und Wechselströme sind im einfachsten Fall sinusförmig. Warum? Weil kompliziertere periodische Signale die Summe von Sinus-Funktionen unterschiedlicher Frequenzen sind (s. die Serie über Fourier-Reihen). Die einfachste Möglichkeit ist also ein Sinus mit einer Frequenz.

Da die Spannung u(t) (in V) und die Stromstärke i(t) (in A) vom selben elektromagnetischen Wechselfeld erzeugt werden, haben sie auch dieselbe Frequenz. Allerdings können sie zeitlich verschoben sein, müssen also nicht dieselbe Phase haben. Ein solches Beispiel ist in Abb. 1 gezeigt.

AnimUIZeiger — Abb. 1: Zeitlicher Verlauf von Spannung u und Stromstärke i bei einer idealen Luftspule.

Fourier-Reihen, Teil 2 – Das Spektrum

In Teil 1 haben wir gesehen, dass die Projektion der Summe rotierender Zeiger eine periodische Funktion ergeben kann, wenn die Frequenzen der einzelnen Zeiger ganzzahlige Vielfache der Frequenz des langsamsten Zeigers sind.

In diesem Beitrag werden wir ein paar weitere Beispiele sehen und uns die komplexen Amplituden $\underline{A}_k$ der einzelnen Zeiger genauer ansehen. Die Menge dieser $\underline{A}_k$ einer Funktion f ist das Spektrum von f.

Fourier-Reihen, Teil 1 – Addition rotierender Zeiger

In Teil 6 der Serie über komplexe Zahlen haben wir Zeiger besprochen, die sich mit konstanter Geschwindigkeit im Kreis drehen. Die Projektion so eines Zeigers entlang der reellen Achse ergab eine zeitabhängige Funktion – die allgemeine Sinus-Funktion.

Was passiert, wenn wir – wie in Abb. 1 gezeigt – mehrere solche Zeiger addieren? Welche Funktionen ergeben sich aus der Projektion des Summenzeigers?

ZeigerSin1Sin2 — Abb. 1: Addition verschieden schnell rotierender Zeiger. Der rote Summenzeiger läuft nicht mehr auf einem Kreis, sondern entlang einer Epizykloide.

Komplexe Zahlen, Teil 6b – die allgemeine Sinus-Funktion

Im letzten Teil haben wir gesehen, wie rotierende Zeiger mit der Sinus-Funktion zusammenhängen. Wir konnten die Kreisfrequenz $\omega$ , die Amplitude $A$ , die Phase $\varphi$ oder den Mittelwert $m$ vorgeben.

Oder wir geben alle vier Parameter gleichzeitig vor, was uns zur allgemeinen Sinus-Funktion

$\Im\left(\underline{A}e^{\underline{i}\omega t} + m\underline{i}\right) = \Im\left(A e^{\underline{i} (\omega t + \varphi)} + m\underline{i}\right) = A\sin(\omega t + \varphi) + m$

führt. Ein Beispiel dafür zeigt Abb. 1.

ZeigerAllgSin — Abb. 1: allgemeine Sinus-Funktion mit Amplitude $A = 2$ , Kreisfrequenz $\omega$ , Phase $\varphi = \tau/8 = 45^\circ$ und Mittelwert $m = 1$ .

Abb. 1: allgemeine Sinus-Funktion mit Amplitude $A = 2$ , Kreisfrequenz $\omega$ , Phase $\varphi = \tau/8 = 45^\circ$ und Mittelwert $m = 1$ .

Komplexe Zahlen, Teil 6 – rotierende Pfeile (Zeiger) und trigonometrische Funktionen

Bisher haben wir nur zeitlich fixierte Pfeile in der Ebene betrachtet. Ab jetzt lassen wir sie mit konstanter Geschwindigkeit rotieren – wodurch sie zu Zeigern werden.

Der Pfeil $e^{\underline{i}\,\alpha}$ hatte die Länge (den Betrag) 1 und den Winkel $\alpha$ gegen die reelle Achse $\Re$ (s. Abb. 1). Wenn der Winkel $\alpha$ linear mit der Zeit $t$ zunimmt, kann man ihn als zeitlich veränderlichen Bruchteil der vollen Umdrehung $\tau = 2\pi$ auffassen: