Diskrete Fourier-Transformation (DFT)

Fourier-Reihen, Teil 9b

Zwischendurch eine kurze Animation des Logos meiner Schule:

Details in Teil 9.

Fourier-Reihen, Teil 9 – komplexe Signale und Kurven in der Ebene

In den bisherigen Teilen haben wir uns mit der Fourier-Analyse reeller Signale beschäftigt. Dabei haben wir rotierende Zeiger unterschiedlicher Frequenzen addiert und die Projektion des Summenzeigers ergab unser zeitabhängiges Signal (s. Teil 1).

Der Summenzeiger hat dabei recht komplizierte Kurven in der komplexen Ebene beschrieben (s. speziell Teil 2). In diesem Teil stellen wir nun die Frage, wie wir geschlossene, ebene Kurven in eine Summe von rotierenden Zeigern verwandeln können.

Einfache Beispiele für solche Kurven sind Lissajous-Figuren wie in Abb. 1 gezeigt. Wir betrachten dabei die Bahnkurve eines Punktes, dessen x– und y-Koordinaten allgemeine Sinus-Funktionen der Zeit t sind. Wenn der Quotient der beiden Frequenzen rational ist, sind die Bahnen geschlossen – und damit periodisch.

Abb. 1: Bahn eines Punktes, dessen x– und y-Koordinaten allgemeine Sinus-Funktionen sind. Speziell ist $f'=0.2\,\text{Hz}$ und $f''=0.4\,\text{Hz}$ , was eine Periodendauer von $T=5\,\text{s}$ bedeutet.

Abb. 1: Bahn eines Punktes, dessen x– und y-Koordinaten allgemeine Sinus-Funktionen sind. Speziell ist $f'=0.2\,\text{Hz}$ und $f''=0.4\,\text{Hz}$ , was eine Periodendauer von $T=5\,\text{s}$ bedeutet.

Fourier-Reihen, Teil 7 – wie Signale in Frequenzen zerlegt werden

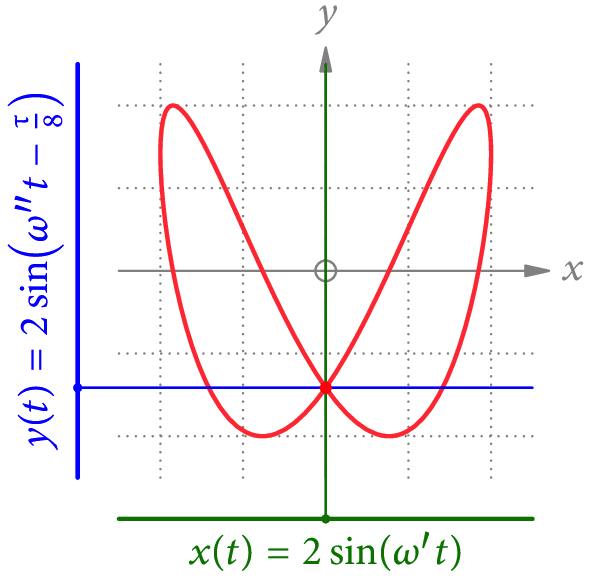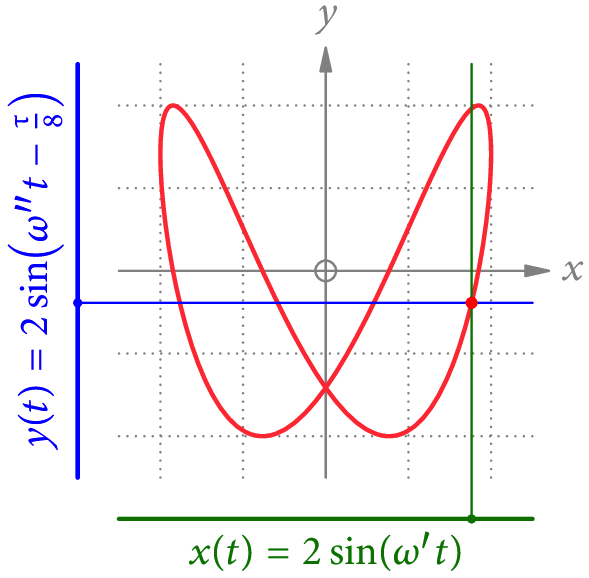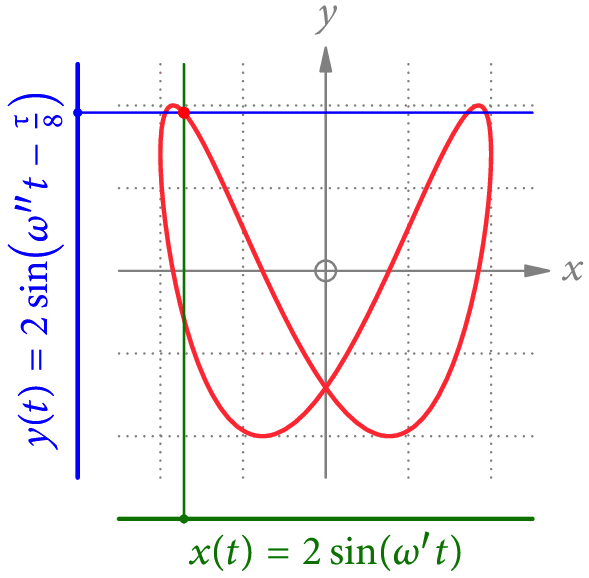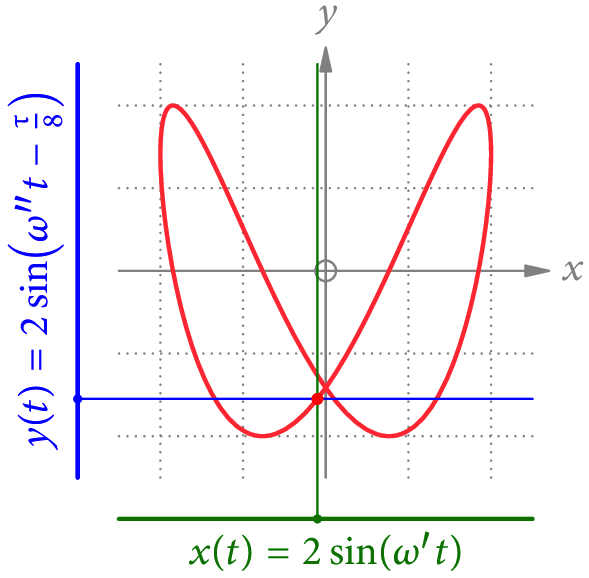
Wenn wir ein Signal in eine Fourier-Reihe »entwickeln«, müssen wir herausfinden, welche Frequenzen in diesem Signal stecken. Die Formeln dazu haben wir schon in Teil 3 gesehen. Aber warum funktioniert das – speziell bei gemessenen Signalen – wirklich?

Fourier-Reihen, Teil 6b – DFT gemessener Signale

Im letzten Teil haben wir die Fourier-Koeffizienten eines Signals s numerisch berechnet, unter der Voraussetzung, die Periodendauer des Signals zu kennen.

Wenn wir ein Signal messen, kennen wir dessen Periodendauer normalerweise nicht. Wir messen einfach während der Messdauer $T_m$ mit der Sampling-Frequenz (Abtastrate) $f_s$ die momentanen Werte $s(t)$ . Wie beeinflusst das die Fourier-Koeffizienten?

Abb. 1 zeigt nochmals unser Signal

$s(t) = -1 + 3\sin(2\pi \cdot 0.5\,\text{Hz} \cdot t + \pi) + 2\sin(5 \cdot 2\pi \cdot 0.5\,\text{Hz} \cdot t - \tfrac{\pi}{2})$

aus dem letzten Teil.

sampled_meas_sig — Abb. 1: Das Signal aus Teil 6. Innerhalb der Messdauer von 3.5 s ist das Signal dicker gezeichnet. Der hellblaue Verlauf ist die tatsächliche Periodizität, der hellrote Verlauf die scheinbare Periodizität. Die roten Punkte sind die 32 Messwerte.

Fourier-Reihen, Teil 6 – Diskrete Fourier-Transformation (DFT)

In Teil 3 haben wir gesehen, dass wir ein periodisches Signal s mit Periodendauer T als Summe rotierender Zeiger

$\displaystyle s(t) = \sum_{-\infty}^{+\infty}\underline{S}_k \cdot e^{\underline{i}k\omega_1 t}$

schreiben können (zumindest wenn s »schön« ist). Dabei ist die Grundfrequenz $f_1 = 1/T$ und die Grundkreisfrequenz $\omega_1 = \tau/T$ mit $\tau = 2\pi$ .

Wir haben auch gesehen, dass wir die Fourier-Koeffizienten $\underline{S}_k$ über die Mittelwerte

$\displaystyle\underline{S}_k = \frac{1}{T} \int_0^T s(t) \cdot e^{-\underline{i}k\omega_1 t} \, \mathrm{d}t$

erhalten. Dabei müssen wir über eine ganze Periode integrieren, egal wo wir anfangen: 0 bis T, $-T/2$ bis $+T/2$ , $-T/4$ bis $+3T/4$ , …

Wenn wir den Verlauf des Signals s tatsächlich als mathematischen Funktionsterm kennen, sind diese Integrale prinzipiell berechenbar – auch wenn es manchmal kompliziert werden kann. Aber was, wenn wir den Funktionsterm des Signals nicht kennen, z.B. weil wir es gemessen haben? – In beiden Fällen können wir die Integrale zumindest näherungsweise numerisch berechnen.