Fourier-Reihen, Teil 1 – Addition rotierender Zeiger

In Teil 6 der Serie über komplexe Zahlen haben wir Zeiger besprochen, die sich mit konstanter Geschwindigkeit im Kreis drehen. Die Projektion so eines Zeigers entlang der reellen Achse ergab eine zeitabhängige Funktion – die allgemeine Sinus-Funktion.

Was passiert, wenn wir – wie in Abb. 1 gezeigt – mehrere solche Zeiger addieren? Welche Funktionen ergeben sich aus der Projektion des Summenzeigers?

ZeigerSin1Sin2 — Abb. 1: Addition verschieden schnell rotierender Zeiger. Der rote Summenzeiger läuft nicht mehr auf einem Kreis, sondern entlang einer Epizykloide.

Kreisende Kreise

Bei der Addition wird ein Pfeil an das Ende des anderen parallel verschoben. Dadurch wird auch der Mittelpunkt des Kreises, auf dem ein Zeiger rotiert an die Spitze des anderen rotierenden Zeigers verschoben. Man erhält so Kreise, die umeinander kreisen – der Summenzeiger beschreibt eine Epizykloide. Für den speziellen Fall aus Abb. 1 ist es eine Herzkurve (Kardioide).

Aufgrund der Kommutativität der Addition ist es egal, welcher Kreis um welchen kreist (s. Abb 2). Normalerweise laufen jedoch die schnelleren um die langsameren Kreise.

ZeigerSin2Sin1 — Abb. 2: Die Kommutativität der Addition gilt auch für rotierende Zeiger.

In jedem Fall ändern sich sowohl die Länge als auch die Geschwindigkeit des Summenzeigers während einer Periode.

Frequenzen und Periodizität

Wenn beide rotierende Zeiger dieselbe Frequenz haben, sind wir wieder bei dem Fall am Ende von Teil 6 über komplexe Zahlen: die Summe ist ein rotierende Zeiger mit derselben Frequenz aber ev. einer anderen Amplitude und Phase. Das bringt nichts wirklich Neues.

In Abb. 1 hat der große Zeiger eine Periodendauer von 2 s; der kleine Zeiger hat die halbe Amplitude und die halbe Periodendauer (die doppelte Frequenz). Während der große Zeiger eine volle Umdrehung macht, macht der kleine Zeiger zwei volle Umdrehungen – und beide sind in derselben Stellung wie zu Beginn. Der Summenzeiger vollführt also eine periodische Bewegung, deren Periodendauer durch den langsameren Zeiger bestimmt ist.

Diese einfache Situation (kompliziertere kommen später) hat man immer, wenn man zu einem langsamen Zeiger mit der Grundfrequenz $f_1 = 1/T$ weitere Zeiger addiert, deren Frequenzen ganzzahlige Vielfache der Grundfrequenz sind. Die Projektion des langsamsten Zeigers ist die Grundschwingung, die Projektionen der schnelleren Zeiger sind die Oberschwingungen. In der Akustik würde man von Grundton und Obertönen sprechen.

In unserem Beispiel ist die Grundfrequenz $f_1 = \frac{1}{T} = \frac{1}{2\,\text{s}} = 0.5\,\text{Hz}$ und die Grundkreisfrequenz $\omega_1 = \tau \cdot f_1 \approx 3.14\,\text{s}^{-1}$ . Die erste Oberschwingung hat die Frequenz $f_2 = 2 \cdot f_1 = 2 \cdot 0.5\,\text{Hz} = 1\,\text{Hz}$ . Der Summenzeiger ist dann

$\displaystyle \underline{z}(t) = e^{\underline{i}\omega_1 t} + \tfrac{1}{2}\,e^{\underline{i}2\omega_1 t}$ .

Projektion des Summenzeigers

Die Projektion ist der Imaginärteil der Summe – was dasselbe ist, wie die Summe der einzelnen Imaginärteile:

$\displaystyle\begin{aligned}f(t) = \Im\left(\underline{z}(t)\right) &= \Im\left(e^{\underline{i}\omega_1 t} + \tfrac{1}{2} \, e^{\underline{i}2\omega_1 t}\right) \\ &= \Im\left(e^{\underline{i}\omega_1 t}\right) + \Im\left(\tfrac{1}{2} \, e^{\underline{i}2\omega_1 t}\right) \\ &= \sin(\omega_1 t) + \tfrac{1}{2}\sin(2\omega_1 t)\end{aligned}$

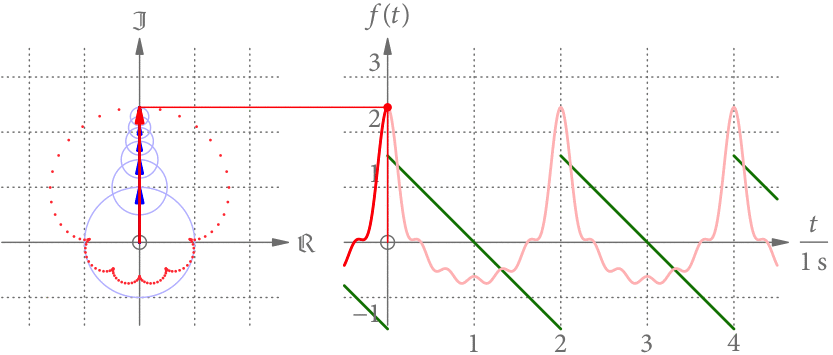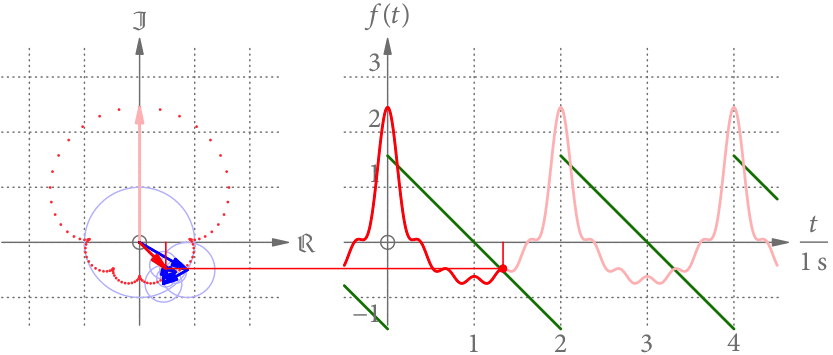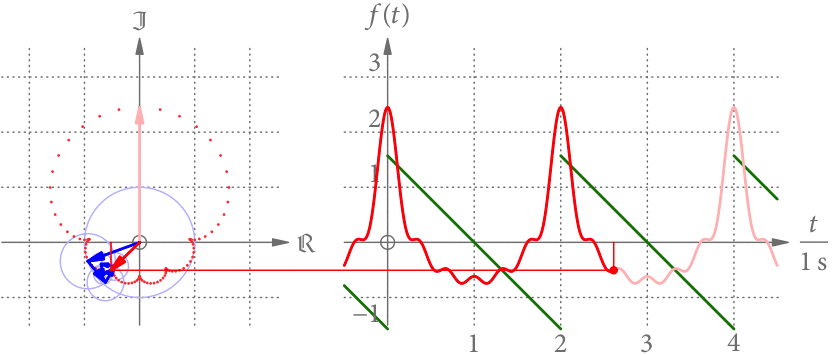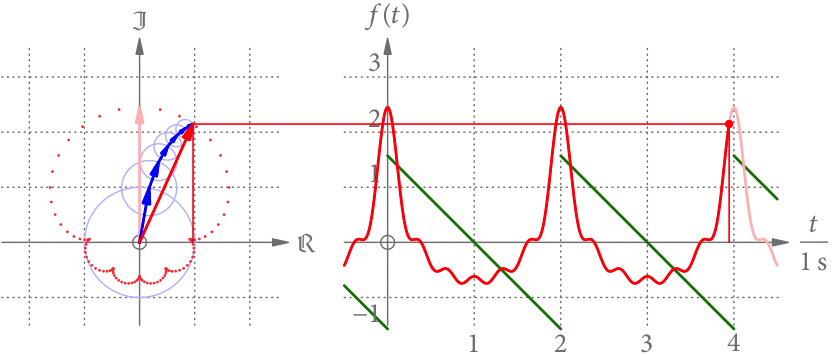
Der linke Teil von Abb. 3 zeigt die Summenkurve als Punkte im Zeitabstand von 0.02 s. Je größer der Abstand der Punkte, desto schneller dreht sich der Summenzeiger in diesem Bereich. Offensichtlich dreht er sich nicht mehr mit konstanter Geschwindigkeit.

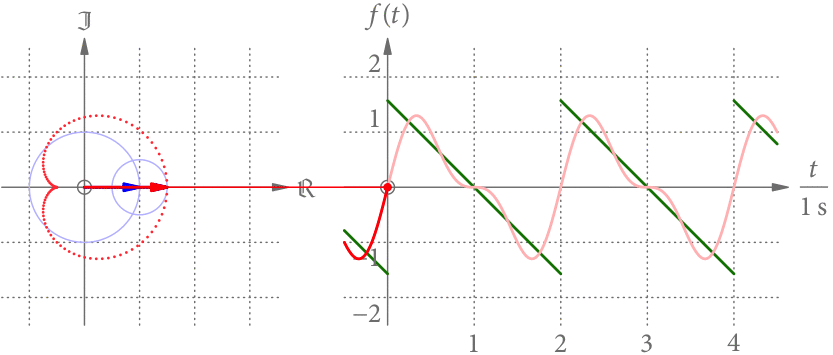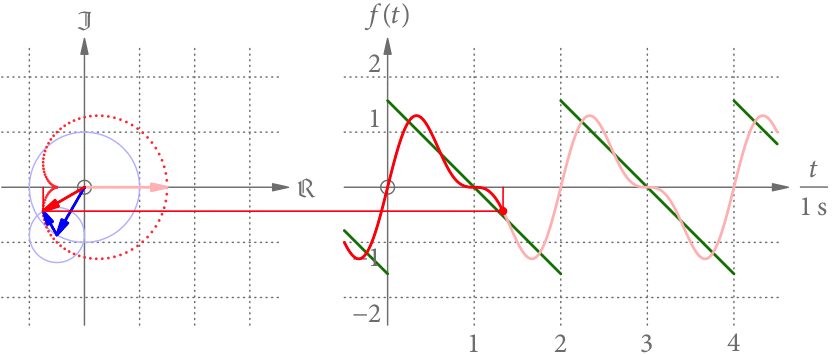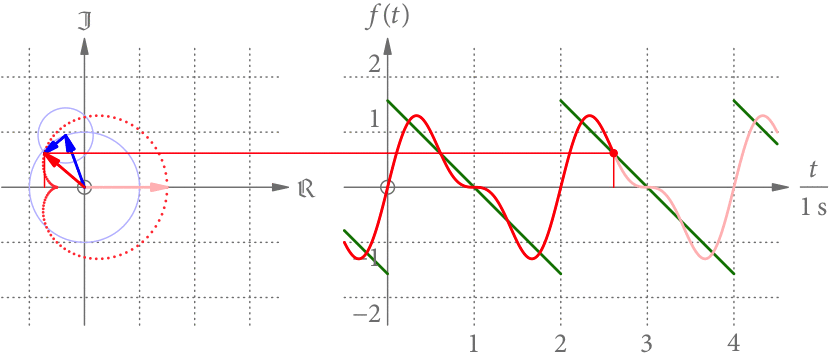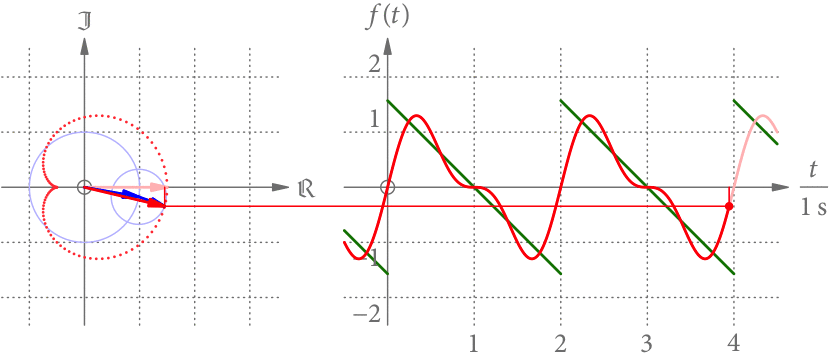
AnimSawTooth2 — Abb. 3: Links: Die Epizykloide ist durch Punkte mit Zeitabstand 0.02 s dargestellt. Rechts: Die Projektion $\sin\left(\omega_1 t\right) + \frac{1}{2}\sin\left(2\omega_1 t\right)$ ist eine Näherung der grünen periodischen Funktion.

Abb. 3: Links: Die Epizykloide ist durch Punkte mit Zeitabstand 0.02 s dargestellt. Rechts: Die Projektion $\sin\left(\omega_1 t\right) + \frac{1}{2}\sin\left(2\omega_1 t\right)$ ist eine Näherung der grünen periodischen Funktion.

Der rechte Teil von Abb. 3 zeigt die Projektion des Summenzeigers als Funktion der Zeit. Wir bekommen eine periodische Funktion mit Periodendauer 2 s. Diese Projektion hat eine gewisse Ähnlichkeit zu der grün gezeichneten, stückweise linearen Funktion.

Was, wenn wir das Spiel weiter spielen? Wir haben den doppelt so schnellen Zeiger mit der halben Länge addiert. Was, wenn wir noch einen 3-mal so schnellen Zeiger mit einem Drittel der Länge addieren, einen 4-mal so schnellen Zeiger mit einem viertel Länge, …

$\displaystyle f(t) = \Im\left(\sum_{k=1}^\infty\tfrac{1}{k} \, e^{\underline{i}k\omega_1 t}\right) = \sum_{k=1}^\infty\Im\left(\tfrac{1}{k} \, e^{\underline{i}k\omega_1 t}\right) = \sum_{k=1}^\infty\tfrac{1}{k}\sin(k\omega_1 t)$

Das Ergebnis bis zur 6-fachen Grundfrequenz zeigt Abb. 4 – der Summenzeiger beschreibt in der komplexen Ebene keine einfache Kardioide mehr, sondern eine Kurve, die aussieht wie eine Muschel. Links von der imaginären Achse wirbeln die Kreise wild umeinander, sodass sich in der Projektion eine fast lineare Funktion ergibt.

AnimSawTooth6 — Abb. 4: Addiert man insgesamt 6 Zeiger nach dem Schema aus Abb. 2, erhält man eine Projektion, die noch viel besser zu der grünen periodischen Funktion passt. Die Punkte der Summenkurve haben wieder 0.02 s Zeitabstand.

Rechts von der imaginären Achse zeigen die Zeiger ungefähr in dieselbe Richtung, sodass sich ihre Winkelgeschwindigkeiten addieren. Dadurch dreht sich der Summenzeiger in diesem Bereich sehr schnell, und in der Projektion erhalten wir den benötigten Sprung in der grünen Funktion. Würden wir weitere Zeiger addieren, würde sich die Summenkurve immer weiter nach rechts ausdehnen und der Summenzeiger sich immer schneller drehen.

zeitliche Verschiebung

Um die Sinus-Funktion in der Zeit zu verschieben, mussten wir den Zeiger um einen entsprechenden fixen Winkel vor- bzw. zurückdrehen.

Wenn wir hier jetzt jeden Zeiger einfach um z.B. $\frac{\tau}{4} = 90^\circ$ vordrehen – um die Funktion eine viertel Periode in der Zeit nach vorne zu schieben – drehen wir die gesamte Summenkurve um $\frac{\tau}{4} = 90^\circ$ um den Ursprung. Weil diese Kurve asymmetrisch ist, ändert sich dadurch aber die Projektion entlang der reellen Achse. Wir erhalten so also eine völlig andere periodische Funktion (s. Abb. 5).

AnimSawTooth690f — Abb. 5: Dreht man einfach alle Einzelzeiger um $\frac{\tau}{4} = 90^\circ$ vor, ergibt sich in der Projektion eine völlig andere periodische Funktion.

Um es richtig zu machen, erinnern wir uns daran, dass die Phase $\varphi$ über

$\varphi = -\frac{\tau}{T} \cdot \Delta t= -\omega \cdot \Delta t$

mit der Zeitverschiebung $\Delta t$ zusammenhängt. Wenn unsere Kreisfrequenz $\omega$ also verdoppelt wird, müssen wir auch um den doppelten Winkel verdrehen, bei der dreifachen Kreisfrequenz um den dreifachen Winkel usw.

Wir haben dann die Summe

$\displaystyle\underline{s}(t) = \sum_{k=1}^\infty \tfrac{1}{k} \, e^{\underline{i}(k\omega_1 t - k\omega_1 \Delta t)} = \sum_{k=1}^\infty \tfrac{1}{k} \, e^{\underline{i}k\omega_1(t - \Delta t)} = \underline{z}(t - \Delta t)$ ,

die gleich unserer vorigen Summe, aber zu einem anderen Zeitpunkt ist. Wir haben also die zeitliche Nummerierung der Punkte unserer Summenkurve verändert, aber nicht die Kurve selber. Abb. 6 zeigt das für $\Delta t = -T/4 = -0.5\,\text{s}$ .

AnimSawTooth690r — Abb. 6: Dreht man den Zeiger mit der $k$ -fachen Frequenz um $k \cdot \frac{\tau}{4} = k \cdot 90^\circ$ vor, läuft die Funktion um $\frac{T}{4} = 0.5\,\text{s}$ zeitlich vor.

Abb. 6: Dreht man den Zeiger mit der $k$ -fachen Frequenz um $k \cdot \frac{\tau}{4} = k \cdot 90^\circ$ vor, läuft die Funktion um $\frac{T}{4} = 0.5\,\text{s}$ zeitlich vor.

Diskussion

Durch Addition verschieden schnell rotierender Zeiger – deren Frequenzen ganzzahlige Vielfache einer Grundfrequenz sind – konnten wir in der Projektion schon ein paar periodische Funktionen annähern. Im nächsten Teil wird es weitere Beispiele dazu geben.

Da stellt sich natürlich umgekehrt die Frage: Wenn wir irgendeine periodische Funktion $f$ haben, können wir die immer als die Summe

$\displaystyle f(t) = \Im\left(\sum_{k = 0}^\infty \underline{A}_k e^{\underline{i}k\omega_1 t}\right)$

schreiben? Und wo bekommen wir die komplexen Amplituden $\underline{A}_k$ her? Konvergiert die Reihe auf der rechten Seite überhaupt – und wenn ja, wohin? In den folgenden Teilen werde ich auf diese Fragen eingehen.

Wer nach diesem Herumwirbeln von Kreisen in der komplexen Ebene meint, dass Fourier-Reihen etwas mit der Epizykeltheorie des Ptolemäischen Weltbildes zu tun haben, hat nicht ganz unrecht. Auch damit werden wir uns später noch beschäftigen (s. Teil 9).

Weiter in Teil 2.