Physik – Seite 2 – Herr Fessa

Fourier-Reihen, Teil 5 – Schwebungen

In Teil 1 haben wir gesehen, dass die Addition von Sinussignalen unterschiedlicher Frequenzen wieder ein periodisches Signal ergibt, wenn alle Frequenzen ganzzahlige Vielfache einer Grundfrequenz $f_1$ sind. Die Periodendauer des Summensignals ist dann $T = 1/f_1$ . In diesem Teil beschäftigen wir uns mit Frequenzen, die nicht mehr ganzzahlige Vielfache voneinander sind.

Zeiger und Wechselspannungen bzw. Wechselströme

(2023-11-03: Videos zur Motivation komplexer Zahlen mit Wechselströmen gibt es hier auf Deutsch und hier auf Englisch.)

(2018-05-21 überarbeitet) Wechselspannungen und Wechselströme sind im einfachsten Fall sinusförmig. Warum? Weil kompliziertere periodische Signale die Summe von Sinus-Funktionen unterschiedlicher Frequenzen sind (s. die Serie über Fourier-Reihen). Die einfachste Möglichkeit ist also ein Sinus mit einer Frequenz.

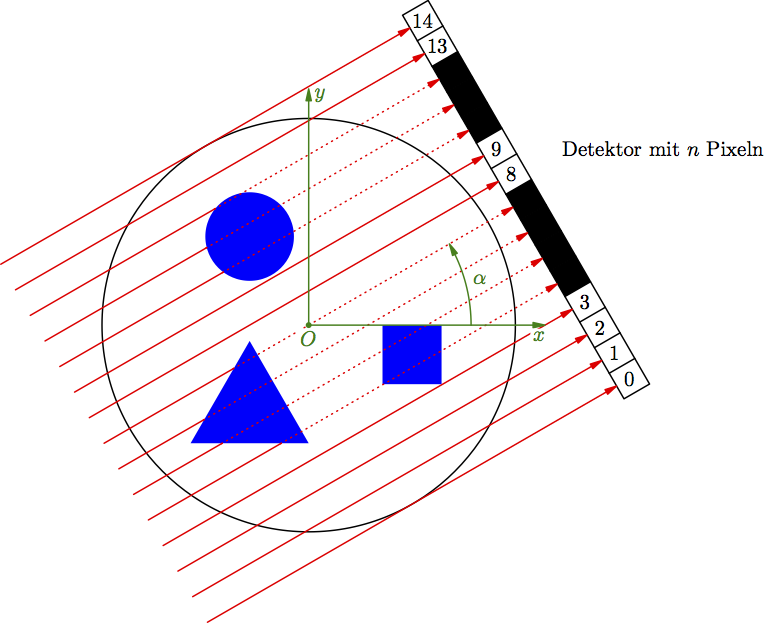
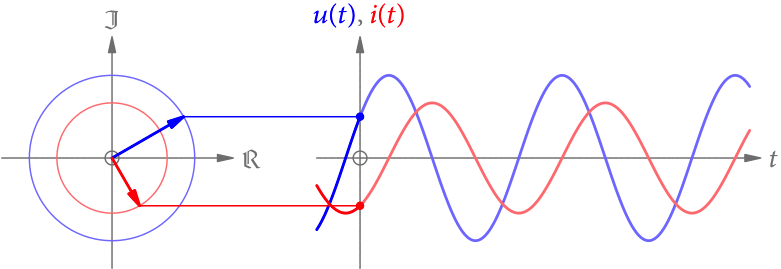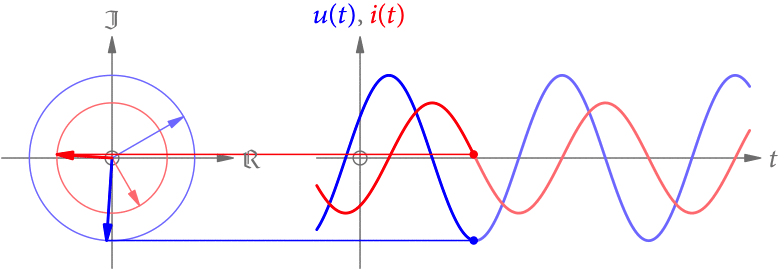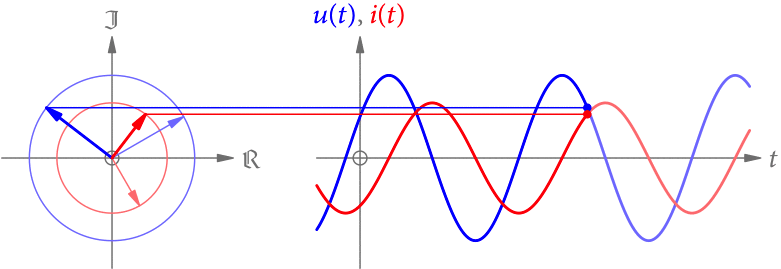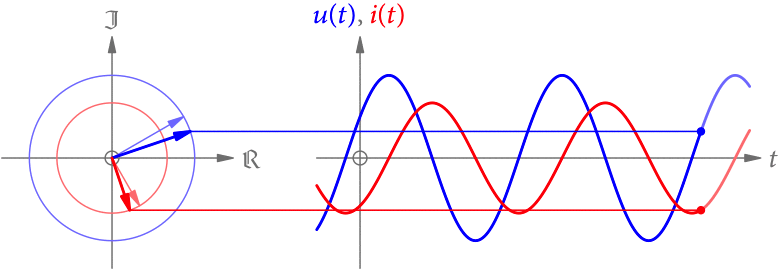
Da die Spannung u(t) (in V) und die Stromstärke i(t) (in A) vom selben elektromagnetischen Wechselfeld erzeugt werden, haben sie auch dieselbe Frequenz. Allerdings können sie zeitlich verschoben sein, müssen also nicht dieselbe Phase haben. Ein solches Beispiel ist in Abb. 1 gezeigt.

AnimUIZeiger — Abb. 1: Zeitlicher Verlauf von Spannung u und Stromstärke i bei einer idealen Luftspule.

Computertomographie (CT), Teil 8

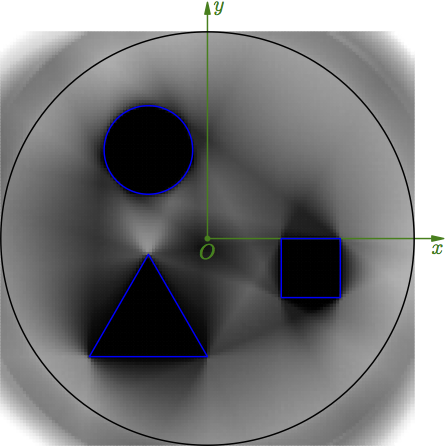
Im letzten Teil haben wir gesehen, dass Objekte Licht in unterschiedlichem Ausmaß durchlassen können. Im Folgenden werden wir uns nur mit Absorption beschäftigen. Abb. 1 zeigt unsere bereits aus Teil 1 bekannten Objekte, allerdings mit unterschiedlichen Absorptionskoeffizienten. Zusätzlich ist der Kreis jetzt ein innen hohler Kreisring. Die Detektorpixel sind jetzt nicht mehr nur schwarz/weiß, sondern zeigen auch Helligkeiten dazwischen.

SetupParallelAbs — Abb. 1: Drei Objekte mit unterschiedlichen Absorptionskoeffizienten, eines davon hohl. Das Dreieck hat $\mu = 0.8\,\text{cm}^{-1}$ , der Kreisring hat $\mu = 0.6\,\text{cm}^{-1}$ und das Quadrat hat $\mu = 0.4\,\text{cm}^{-1}$ .

Abb. 1: Drei Objekte mit unterschiedlichen Absorptionskoeffizienten, eines davon hohl. Das Dreieck hat $\mu = 0.8\,\text{cm}^{-1}$ , der Kreisring hat $\mu = 0.6\,\text{cm}^{-1}$ und das Quadrat hat $\mu = 0.4\,\text{cm}^{-1}$ .

Weiterlesen „Computertomographie (CT), Teil 8“

Computertomographie (CT), Teil 7

Bisher haben wir angenommen, dass ein Detektor-Pixel entweder die komplette Lichtintensität »sieht«, oder gar nichts (Schatten). Wie so oft ist diese Schwarz-Weiß-Malerei unrealistisch.

Warum wird es finster?

Ohne Objekte zwischen Strahlungsquelle und Detektor sieht jeder Detektor-Pixel die volle Lichtintensität (Helligkeit) $I_0$ . Mit Objekten dazwischen sieht dieser Pixel die Intensität $I$ , die im Allgemeinen kleiner als $I_0$ ist.

Weiterlesen „Computertomographie (CT), Teil 7“

Computertomographie (CT), Teil 6

Eine Linie aus kleinen Quadraten

In Teil 5 haben wir die Rasterung besprochen und gesehen, wie man Punkt-Koordinaten in der »realen« Welt in Pixel-Koordinaten umrechnet. Jetzt müssen wir diese Punkte durch eine Linie aus Pixeln verbinden (s. Abb. 1). Die Pixel, in denen die Punkte $P$ und $Q$ liegen, gehören auf jeden Fall dazu. Aber welche noch?

Linie1 — Abb. 1: Durch welche Pixel geht die Verbindungslinie von $P$ und $Q$ ?

Abb. 1: Durch welche Pixel geht die Verbindungslinie von $P$ und $Q$ ?

Dieses Problem trat schon zu Beginn der Computergraphikära auf und wurde in den verschiedensten Varianten gelöst. Im Folgenden besprechen wir eine Variante des Bresenham-Algorithmus für Linien.

Weiterlesen „Computertomographie (CT), Teil 6“

Computertomographie (CT), Teil 5

Der diskrete Charme der Pixel

Wie schon gesagt, muss man für die Rückprojektion der Schattenbilder ein Pixel-Gitter über die reale physikalische Szene legen (s. Abb. 1). Man spricht dabei von Rasterung. Nachdem es sich um eine kreisförmige Szene mit Radius $r$ handelt, ist das Gitter sinnvollerweise quadratisch, und die Anzahl der Pixel in $x$ – und $y$ -Richtung wird gleich gewählt, also $n_x = n_y = n$ . Die Pixel sind dann Quadrate mit einer realen Seitenlänge von $s = 2 r / n$ . Um die Formeln etwas zu vereinfachen wählen wir für $n$ eine gerade Zahl, was keine große Einschränkung bedeutet.

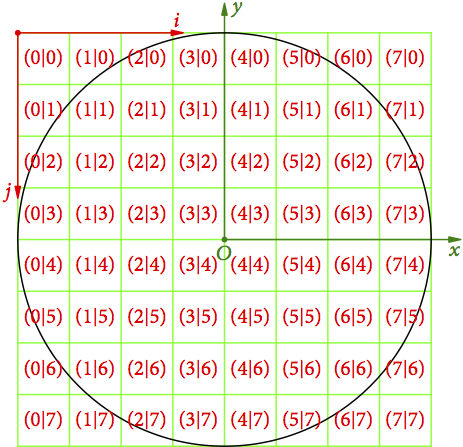
Gitter1 — Abb. 1: Das kreisförmige Gebiet mit Radius $r$ wird mit einem (8×8)-Pixelgitter überdeckt. Der Ursprung des Pixel-Koordinatensystems befindet sich links oben. Die $i$ -Achse zeigt wie die $x$ -Achse nach rechts, die $j$ -Achse zeigt entgegen der $y$ -Achse nach unten.

Abb. 1: Das kreisförmige Gebiet mit Radius $r$ wird mit einem (8×8)-Pixelgitter überdeckt. Der Ursprung des Pixel-Koordinatensystems befindet sich links oben. Die $i$ -Achse zeigt wie die $x$ -Achse nach rechts, die $j$ -Achse zeigt entgegen der $y$ -Achse nach unten.

Weiterlesen „Computertomographie (CT), Teil 5“

Computertomographie (CT), Teil 4

In Teil 3 haben wir aus unseren »Schattenmessungen« ein sehr grobes Bild unserer Objekte rekonstruiert. Im Folgenden sehen wir uns einige bessere Rekonstruktionen an.

BackProjParallel_512_0.5Deg_128x128 — Abb. 1: (128×128)-Pixel Rekonstruktion der Messung mit einem 512-Pixel Detektor und 0.5° Winkelauflösung.

Weiterlesen „Computertomographie (CT), Teil 4“

Computertomographie (CT), Teil 3

Rückprojektion (backprojection)

In Teil 1 ging es um die grundsätzliche Funktionsweise eines CT. In Teil 2 haben wir verschiedene Radon-Transformationen unserer Objekte gesehen.

Jetzt geht es darum, wie wir die Lage und Form unserer Objekte aus der Radon-Transformation rekonstruieren können. Es gibt mehrere Methoden, aber eine der einfachsten – und auch (mit Verbesserungen) in medizinischen CTs verwendete – ist die Rückprojektion (backprojection).

Weiterlesen „Computertomographie (CT), Teil 3“

Computertomographie (CT), Teil 2

Radon-Transformation

In Teil 1 haben wir gesehen, das bei einem CT »Schattenbilder« aus verschiedenen Richtungen gemessen werden. Alle Schattenbilder aus verschiedenen Richtungen zusammen nennt man die Radon-Transformation unserer Objekte.

Weiterlesen „Computertomographie (CT), Teil 2“

Computertomographie (CT), Teil 1

Dieser Eintrag startet eine Serie von Beiträgen zur Computertomographie. Ziel ist es, im Rahmen einer HTL-Diplomarbeit ein (2-dimensionales) CT mit sichtbarem Licht zu bauen.

Setup

Das Grundprinzip ist in Abb. 1 gezeigt. In einer Ebene befinden sich verschiedene Objekte (blau), die mehr oder weniger Licht durchlassen. Aus einer bestimmten Richtung fallen parallele Lichtstrahlen (rot) ein, wodurch die Objekte einen Schatten auf einen Lichtdetektor werfen. Im medizinischen Bereich handelt es sich bei dem Licht um Röntgenstrahlen, aber das Grundprinzip ist für sichtbares Licht identisch.

Weiterlesen „Computertomographie (CT), Teil 1“