Komplexe Zahlen, Teil 7 – Addition in Polardarstellung

Die Polardarstellung komplexer Zahlen (s. Teil 3) ist besonders gut geeignet für Multiplikationen, Divisionen, Potenzen und Wurzeln komplexer Zahlen. Additionen und Subtraktionen sind nicht so einfach.

Mit etwas gutem Willen, geht es aber doch (s. Abb. 1) und führt zu interessanten Resultaten.

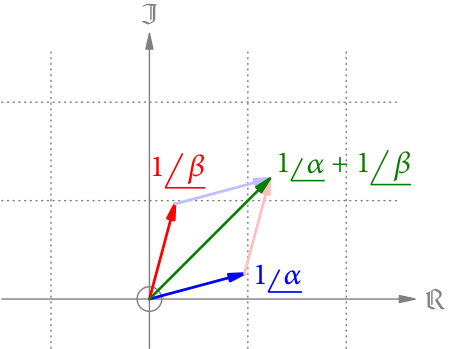
polar_add — Abb. 1: Addition in Polardarstellung; hier am Beispiel $1\angle15^\circ + 1\angle75^\circ = \sqrt{3}\angle45^\circ$ .

Abb. 1: Addition in Polardarstellung; hier am Beispiel $1\angle15^\circ + 1\angle75^\circ = \sqrt{3}\angle45^\circ$ .

Pfeile gleicher Länge

Addition

Abb. 1 zeigt die Addition der komplexen Zahlen $1\angle\alpha$ und $1\angle\beta$ . Weil beide Pfeile die Länge 1 haben, entsteht durch die Parallelverschiebung der Addition eine Raute – d.h. ein Parallelogramm mit vier gleich langen Seiten. Die Summe ist die Diagonale dieser Raute und halbiert damit den Winkel zwischen den Seiten $1\angle\alpha$ und $1\angle\beta$ . Sprich, der Summenpfeil zeigt in die Richtung $\frac{\alpha + \beta}{2}$ .

Die Stärke der Polardarstellung ist die einfache Multiplikation: Länge mal Länge und Winkel plus Winkel. Wir versuchen jetzt, unsere beiden Pfeile $1\angle\alpha$ und $1\angle\beta$ als Produkt mit einem Pfeil in Richtung der Summe zu schreiben. Offensichtlich gilt

$\alpha = \dfrac{\alpha + \beta}{2} + \dfrac{\alpha - \beta}{2}$ und $\beta = \dfrac{\alpha + \beta}{2} - \dfrac{\alpha - \beta}{2}$ .

Damit haben wir die Faktorisierungen

$1\angle\alpha = 1\angle\left(\dfrac{\alpha + \beta}{2}\right) \cdot 1\angle\left(\dfrac{\alpha - \beta}{2}\right)$

und

$1\angle\beta = 1\angle\left(\dfrac{\alpha + \beta}{2}\right) \cdot 1\angle\left(-\dfrac{\alpha - \beta}{2}\right)$ .

Addieren und Herausheben liefert

$\begin{aligned}1\angle\alpha +1\angle\beta &=1\angle\left(\dfrac{\alpha + \beta}{2}\right) \cdot 1\angle\left(\dfrac{\alpha - \beta}{2}\right) +1\angle\left(\dfrac{\alpha + \beta}{2}\right) \cdot 1\angle\left(-\dfrac{\alpha - \beta}{2}\right) \\ &=1\angle\left(\dfrac{\alpha + \beta}{2}\right) \cdot \left[1\angle\left(\dfrac{\alpha - \beta}{2}\right) +1\angle\left(-\dfrac{\alpha - \beta}{2}\right)\right]\end{aligned}$

Die Summanden in der eckigen Klammer unterscheiden sich nur durch das Vorzeichen des Winkels – d.h., sie sind komplex konjugiert zueinander. Die Summe einer Zahl und ihrer komplex konjugierten ist 2-mal der Realteil der Zahl. Die eckige Klammer ist daher

$2 \cdot \Re\left[1\angle\left(\dfrac{\alpha - \beta}{2}\right)\right] = 2 \cos \left(\dfrac{\alpha - \beta}{2}\right)$ .

Mit der Länge und der Richtung haben wir schließlich die Addition

$\boxed{1\angle\alpha +1\angle\beta = 2 \cos \left(\dfrac{\alpha - \beta}{2}\right)\angle\left(\dfrac{\alpha + \beta}{2}\right)}$ . (*)

Bei der »Länge« müssen wir allerdings etwas vorsichtig sein, weil der Cosinus negativ werden kann. Dieses Minus bekommen wir aber weg, wenn wir den Summenwinkel um 180° vor oder zurück drehen (je nachdem, welcher Winkel dann näher bei 0 ist).

Nehmen wir zuerst das Beispiel aus Abb. 1. Hier sind $1\angle\alpha = 1\angle15^\circ$ und $1\angle\beta = 1\angle75^\circ$ . Die Summe hat daher den Winkel (15° + 75°)/2 = 45° und die Länge $2 \cos\left((15^\circ - 75^\circ)/2\right) = 2 \cos(-30^\circ) = \sqrt{3}$ ; insgesamt also

$1\angle15^\circ + 1\angle75^\circ = \sqrt{3}\angle45^\circ$ .

Das zweite Beispiel zeigt Abb. 2. Hier sind $1\angle\alpha = 1\angle165^\circ$ und $1\angle\beta = 1\angle(-75^\circ)$ . Die Summe hat dann den Winkel (165° – 75°)/2 = 45° und ist gleich

$1\angle165^\circ + 1\angle(-75^\circ) = 2\cos(120^\circ)\angle45^\circ = -1\angle45^\circ = 1\angle(-135^\circ)$ .

Im letzten Schritt haben wir das Minus aus dem Betrag entfernt, indem wir den Winkel um 180° zurückgedreht haben.

Abb. 2: $1\angle165^\circ + 1\angle(-75^\circ) = 1\angle(-135^\circ)$ .

Abb. 2: $1\angle165^\circ + 1\angle(-75^\circ) = 1\angle(-135^\circ)$ .

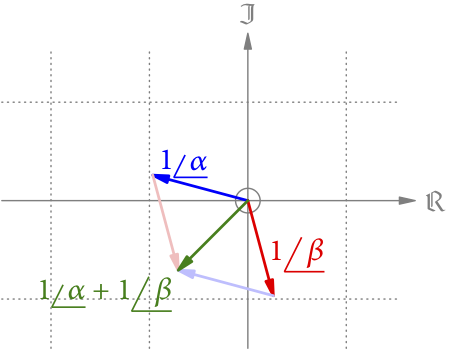
Subtraktion

Wie sieht es bei der Subtraktion aus? Wie in Abb. 3 gezeigt, ist die Subtraktion von $1\angle\beta$ dasselbe wie die Addition von $1\angle(\beta+180^\circ)$ :

$1\angle\alpha - 1\angle\beta = 1\angle\alpha +1\angle(\beta+180^\circ)$ .

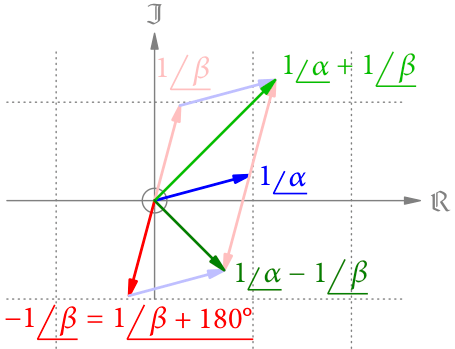
polar_sub — Abb. 3: Subtraktion in Polarkoordinaten; hier am Beispiel $1\angle15^\circ - 1\angle75^\circ = 1\angle(-45^\circ)$ .

Abb. 3: Subtraktion in Polarkoordinaten; hier am Beispiel $1\angle15^\circ - 1\angle75^\circ = 1\angle(-45^\circ)$ .

Weil die Pfeile wieder eine Raute bilden, hat die Differenz die Richtung $(\alpha + \beta + 180^\circ)/2 = (\alpha + \beta)/2 + 90^\circ$ . Spielen wir dasselbe Spiel wie bei der Addition, erhalten wir diesmal

$\begin{gathered}1\angle\alpha - 1\angle\beta = 1\angle\alpha + 1\angle(\beta + 180^\circ) \\ =1\angle\left(\dfrac{\alpha + \beta}{2} + 90^\circ\right) \cdot \left[1\angle\left(\dfrac{\alpha - \beta}{2} - 90^\circ\right) +1\angle\left(-\left(\dfrac{\alpha - \beta}{2} - 90^\circ\right)\right)\right]\end{gathered}$

Die eckige Klammer ist hier

$2 \cdot \Re\left[1\angle\left(\dfrac{\alpha - \beta}{2} - 90^\circ\right)\right] = 2 \cos \left(\dfrac{\alpha - \beta}{2} - 90^\circ\right) = 2\sin \left(\dfrac{\alpha - \beta}{2}\right)$ .

Für die Subtraktion haben wir daher

$\boxed{1\angle\alpha - 1\angle\beta = 2 \sin \left(\dfrac{\alpha - \beta}{2}\right)\angle\left(\dfrac{\alpha + \beta}{2} + 90^\circ\right)}$ . (**)

Falls der Sinus negativ wird, muss der Winkel wieder um $\pm180^\circ$ geändert werden.

Als Beispiel nehmen wir die Subtraktion aus Abb. 3:

$\begin{aligned}1\angle15^\circ - 1\angle75^\circ &= 2 \sin\left(\dfrac{15^\circ - 75^\circ}{2}\right)\angle\left(\dfrac{15^\circ + 75^\circ}{2} + 90^\circ\right)\\ &= 2\sin(-30^\circ)\angle135^\circ = -1\angle135^\circ\\ &= 1\angle(-45^\circ)\end{aligned}$

Überraschende Additionstheoreme

Interessant an der Addition in Polarkoordinaten ist, dass wir daraus überraschende Formeln für die Summen zweier Sinus- bzw. Cosinus-Funktionen bekommen können. Setzen wir die kartesische Darstellung in Glg. (*) ein, ergibt die linke Seite

$\left(\cos(\alpha) + \cos(\beta)\right) + \underline{i}\left(\sin(\alpha) + \sin(\beta)\right)$

und die rechte Seite

$\begin{gathered}2\cos\left(\frac{\alpha - \beta}{2}\right) \cdot \left(\cos\left(\frac{\alpha + \beta}{2}\right) + \underline{i}\sin\left(\frac{\alpha + \beta}{2}\right)\right) \\ = 2\cos\left(\frac{\alpha - \beta}{2}\right) \cdot \cos\left(\frac{\alpha + \beta}{2}\right) + 2\underline{i}\cos\left(\frac{\alpha - \beta}{2}\right) \cdot \sin\left(\frac{\alpha + \beta}{2}\right)\end{gathered}$

Gleichsetzen von Real- und Imaginärteilen führt uns zu den Additionsformeln

$\boxed{\cos(\alpha) + \cos(\beta) =2\cos\left(\dfrac{\alpha - \beta}{2}\right) \cdot \cos\left(\dfrac{\alpha + \beta}{2}\right)}$

und

$\boxed{\sin(\alpha) + \sin(\beta) =2\cos\left(\dfrac{\alpha - \beta}{2}\right) \cdot \sin\left(\dfrac{\alpha + \beta}{2}\right)}$ .

Wenn wir uns daran erinnern, dass eine Drehung um 90° dasselbe ist, wie eine Multiplikation mit $\underline{i}$ , bekommen wir aus der Subtraktionsformel (**)

$\boxed{\cos(\alpha) - \cos(\beta) =-2\sin\left(\dfrac{\alpha - \beta}{2}\right) \cdot \sin\left(\dfrac{\alpha + \beta}{2}\right)}$

und

$\boxed{\sin(\alpha) - \sin(\beta) =2\sin\left(\dfrac{\alpha - \beta}{2}\right) \cdot \cos\left(\dfrac{\alpha + \beta}{2}\right)}$ .

Pfeile unterschiedlicher Länge

Wenn die Pfeile unterschiedliche Länge haben, bilden sie keine Raute mehr (s. Abb. 4, links). Daher funktioniert der Trick mit dem Realteil hier nicht.

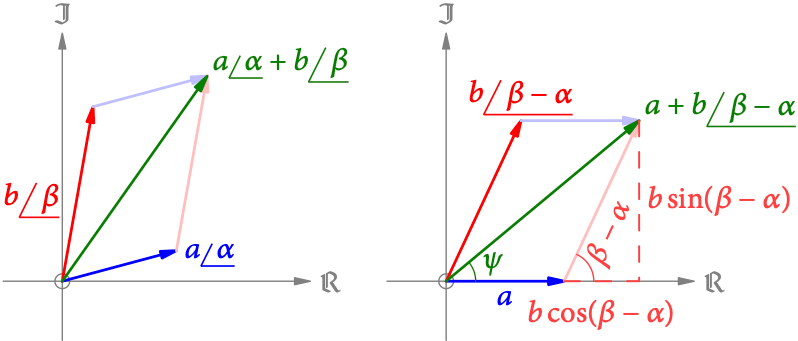
polar_add_ab — Abb. 4: Links: Addition zweier beliebiger Pfeile. Rechts: dieselbe Addition nach Rotation um den Winkel $-\alpha$ .

Wie können aber eine Vereinfachung machen, und z.B. den Winkel $\alpha$ »herausheben« (s. Abb. 4, rechts):

$a\angle\alpha + b\angle\beta = 1\angle\alpha \cdot \bigl(a + b\angle(\beta - \alpha)\bigr)$ .

Die Summe in der Klammer ist die Hypotenuse eines rechtwinkeligen Dreiecks mit den Katheten $a + b\cos(\beta - \alpha)$ und $b\sin(\beta - \alpha)$ . Die Länge der Summe ist daher

$\sqrt{\bigl(a + b\cos(\beta - \alpha)\bigr)^2 + b^2\sin^2(\beta-\alpha)} = \sqrt{a^2 + 2ab\cos(\beta - \alpha) + b^2}$ ,

weil $\cos^2 + \sin^2 = 1$ ist.

Die Richtung der Summe ist $\alpha + \psi$ , wobei gilt:

$\tan(\psi) = \dfrac{b\sin(\beta - \alpha)}{a + b \cos(\beta - \alpha)}$ .

Beim $\arctan$ muss man dann wieder aufpassen, in welchem Quadranten man sich in Abb. 4 (rechts) befindet. Insgesamt haben wir dann

$a\angle\alpha + b\angle\beta =\sqrt{a^2 + 2ab\cos(\beta - \alpha) + b^2}\angle(\alpha + \psi)$ .

Diskussion

Für gleich lange Pfeile ist die Addition in Polarkoordinaten eigentlich gar nicht so schwierig. Für unterschiedliche Längen sieht die Sache leider anders aus. Ich hatte gehofft, eine schönere Herleitung zu finden, aber bin über die Version oben nicht hinaus gekommen.

BTW: Die Addition verschieden langer Pfeile haben wir etwas anders schon am Ende von Teil 6 besprochen.

Ein Gedanke zu „Komplexe Zahlen, Teil 7 – Addition in Polardarstellung“

Fraggle sagt:

14. Oktober 2022 um 14:52

sooo cooool! Da hat sich mal einer diesem Problem angenommen! Alle anderen Mathematiker haben da immer gekniffen. Thanks a lot!

Antworten

Kommentar verfassen Antwort abbrechen

Diese Seite verwendet Akismet, um Spam zu reduzieren. Erfahre, wie deine Kommentardaten verarbeitet werden..