Im Rahmen des Summer of Math Exposition 3 habe ich ein Video zur Einführung komplexer Zahlen über Wechselspannungen und -ströme erstellt (nicht eingebettet).
Die deutsche Version gibt es jetzt auch.
Im letzten Beitrag haben wir begonnen, unsere Kamera zu »bewegen«. Allerdings war sie immer noch relativ groß und sehr nahe an den Objekten dran. In diesem Beitrag werden wir jetzt die Sensorgröße ändern und zoomen – bzw. mit dem Rest der Welt wieder das Gegenteil machen.
Die Animation in Abb. 1 zeigt unser Ziel: Wir simulieren eine Kleinbildkamera mit einem Bildsensor der Größe 36 mm x 24 mm (»full-frame«). Typischerweise kann man dann verschiedene Objektive aufsetzen, die sich in erster Linie durch ihre Brennweiten unterscheiden. Je größer die Brennweite, desto größer der Zoom.
Die Kamera steht an einem fixen Ort und hat zunächst nahe herangezoomt (Brennweite 135 mm). Anschließend zoomt sie heraus (bis Brennweite 24 mm) und dann wieder hinein. Je kleiner die Brennweite, desto kleiner erscheinen die Objekte. Gleichzeitig sieht man mehr von der Umgebung.
Weiterlesen „Malen mit Zahlen, Teil RS5 – Zoomen mit der Kamera“Im letzten Teil haben wir die Objekte in unserer Szene bewegt, indem wir sie mit Transformationsmatrizen aus einer Standardlage heraus verdreht, skaliert und verschoben haben. In diesem Teil werden wir jetzt die Kamera »bewegen« – bzw. den Rest der Welt genau umgekehrt.
Wir wollen uns mit der Kamera durch eine Szene bewegen können, z.B. in einem Flugsimulator. Ein einfaches Beispiel einer bewegten Kamera ist in Abb. 1 gezeigt. Unsere Kamera soll eine Szene umkreisen und immer in deren Mitte schauen. Die Kamera ist dabei etwas unterhalb und zeigt leicht nach oben.
In Teil RS2 haben wir Objekte als Drahtgitter-Modelle fix im Raum dargestellt. In diesem Teil sollen diese Objekte mithilfe der Matrizen aus Teil 2 animiert werden (s. Abb. 1).
Auch dieser Teil ist wieder gemeinsam für Rasterung/Schattierung und Raytracing.
Um Objekte im Raum zu platzieren, müssen wir die Koordinaten ihrer Eckpunkte angeben. Für ein kompliziertes Objekt aus vielen Punkten, das irgendwie im Raum verdreht ist, kann das schwierig werden. Meistens ist es einfacher, die Punkte des Objekts in einer »Standardlage« anzugeben. Von dort aus können wir es in die gewünschte Lage »transformieren«.
Weiterlesen „Malen mit Zahlen, Teil 2 – Transformationen und Matrizen“In Teil 6 der komplexen Zahlen und den bisherigen Teilen zur Fourier-Reihe haben wir uns mit zeitabhängigen Sinus-Funktionen, also zeitlichen Schwingungen, beschäftigt. In diesem Teil soll es um räumliche Schwingungen gehen – in einer und mehr Dimensionen. Den Abschluss bilden dann harmonische Wellen, also Schwingungen, die sich mit der Zeit im Raum ausbreiten.
Abb. 1 zeigt noch einmal eine sinusförmige Schwingung in der Zeit. Wir können sie uns als die Projektion eines rotierenden Zeigers vorstellen, dessen Winkel von der Zeit t abhängt.
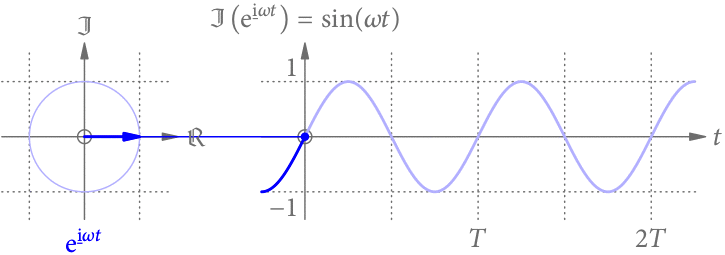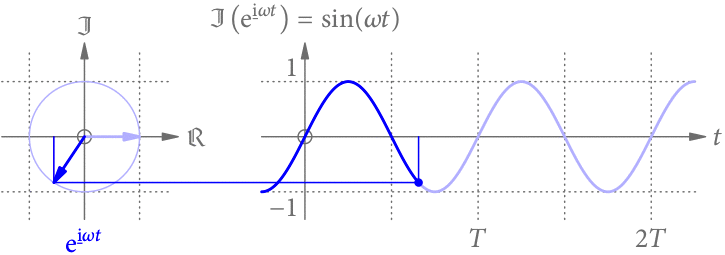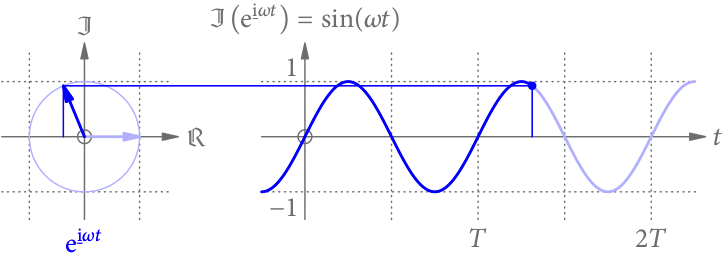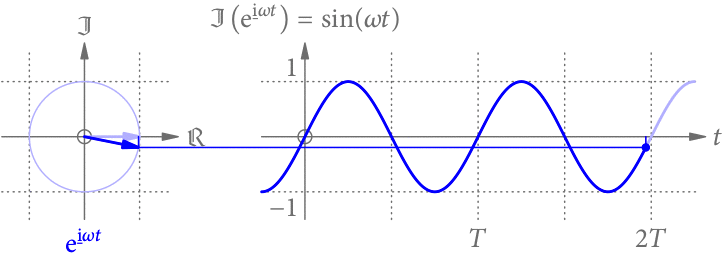
Wir könnten uns aber auch vorstellen, dass der Winkel des Zeigers nicht von der Zeit t, sondern vom Ort x abhängt. Wie Abb. 2 zeigt, ergibt die Projektion dann eine Sinus-Funktion entlang der x-Achse.
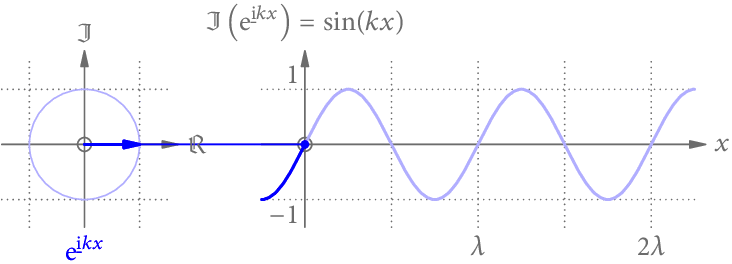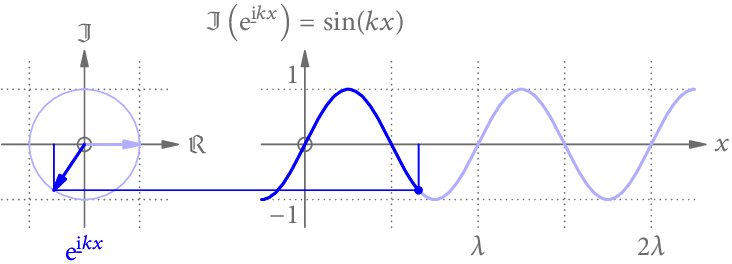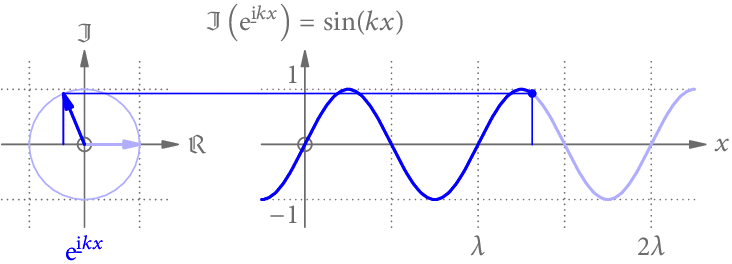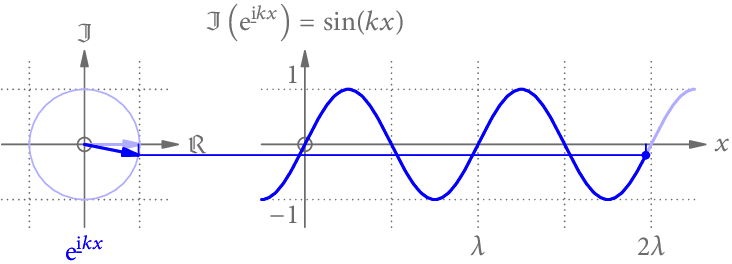
Zwischendurch ein kleine Abschweifung in die geometrische Optik, die für Rasterung/Schattierung und Raytracing gleichermaßen zutrifft.
In Teil 0 haben wir die (inverse) Lochkamera besprochen und wie man damit perspektivische Abbildungen erzeugen kann. Wir sehen die Welt aber mit unseren Augen, die keine Lochkameras sind, sondern eine Linse haben. Ebenso haben (Film-)Kameras mehr oder weniger aufwendige Linsensysteme. Warum funktioniert unser Lochkameramodell dann so gut?
Weiterlesen „Malen mit Zahlen, Teil 1 – Warum funktioniert das Lochkameramodell so gut?“Im letzten Teil haben wir nur Punkte gemalt. In dieser Folge zeichnen wir endlich Linien im Raum. Das ergibt Bilder wie in Abb. 1, in dem die Kanten von drei Würfeln und Breiten-/Längenkreise auf einer Kugel zu sehen sind. Wenn wir Würfel aus kleinen Drahtstücken zusammenlöten, sehen sie so ähnlich aus wie in Abb. 1. Man spricht daher von Drahtgitter- bzw. Wireframe-Modellen.

Punkte haben wir schon projiziert, aber wie projizieren wir Linien im Raum auf den Schirm?
Weiterlesen „Malen mit Zahlen, Teil RS2 – Drahtgittermodelle“Dieser Beitrag liefert den versprochenen Code zum Teil RS1. Geschrieben habe ich ihn in Processing, das im Wesentlichen ein vereinfachtes Java mit ein paar Goodies ist.
Normalerweise veranstalte ich Tagesevents zu 3D-Computergraphik in der letzten Schulwoche. Unsere Schüler können dabei frei aus Events wählen und auch der Klassenverband ist dann aufgelöst. Ich habe also 20+ Teilnehmer aus unterschiedlichen Jahrgängen, Abteilungen und natürlich mit unterschiedlichen Laptops und Betriebssystemen. Manche haben unter Windows noch nie die Kommandozeile gesehen …
Weiterlesen „Malen mit Zahlen, Teil RS1c – Der Code für Kamera und Punkte“