Komplexe Zahlen, Teil 6 – rotierende Pfeile (Zeiger) und trigonometrische Funktionen

Bisher haben wir nur zeitlich fixierte Pfeile in der Ebene betrachtet. Ab jetzt lassen wir sie mit konstanter Geschwindigkeit rotieren – wodurch sie zu Zeigern werden.

Der Pfeil e^{\underline{i}\,\alpha} hatte die Länge (den Betrag) 1 und den Winkel \alpha gegen die reelle Achse \Re (s. Abb. 1). Wenn der Winkel \alpha linear mit der Zeit t zunimmt, kann man ihn als zeitlich veränderlichen Bruchteil der vollen Umdrehung \tau = 2\pi auffassen:

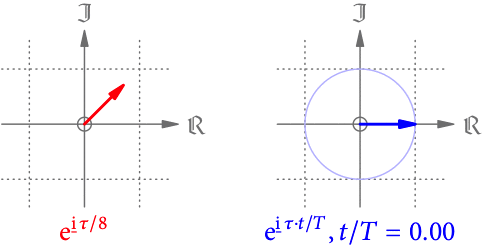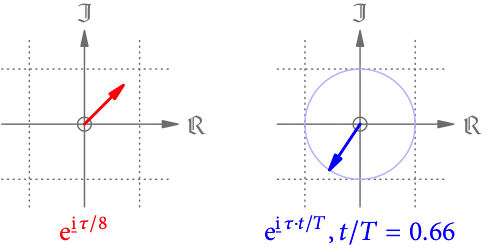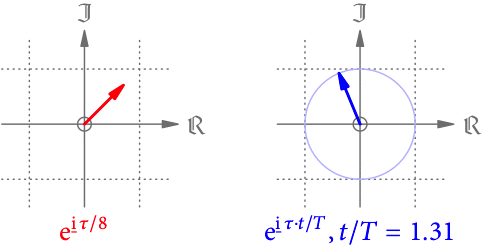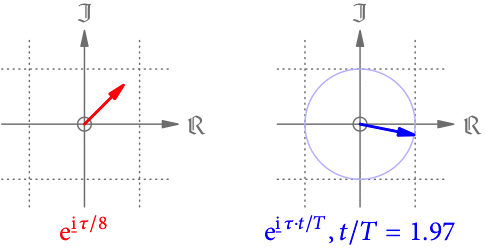
\displaystyle\alpha = \frac{t}{T} \cdot \tau = \frac{\tau}{T} \cdot t .

Abb. 1: Ein Pfeil mit fixem Winkel \alpha = \tau/8 = 45^\circ (links) und ein Zeiger, dessen Winkel linear mit der Zeit zunimmt (rechts). Der mathematisch positive Drehsinn ist gegen den Uhrzeigersinn.

In der Zeit 0 \leq t < T nimmt \alpha jeden Wert von 0 \leq \alpha < \tau an – sprich der Zeiger dreht sich einmal herum und beginnt bei t = T mit einer neuen Umdrehung. Weil sich bei jeder Umdrehung alles periodisch wiederholt, nennt man T die Periodendauer. Die Periodendauer gibt an, wie lange eine Umdrehung dauert. Ihr Kehrwert

\displaystyle f = \frac{1}{T}

wird Frequenz genannt. Die Frequenz gibt an, wie viele Umdrehungen der Zeiger in 1 Sekunde schafft. Das Verhältnis

\displaystyle\omega = \frac{\tau}{T} = \frac{2\pi}{T} = \tau \cdot f = 2\pi \cdot f

nennt man Kreisfrequenz. Die Kreisfrequenz gibt an, welchen Winkel der Zeiger in 1 Sekunde überstreicht.

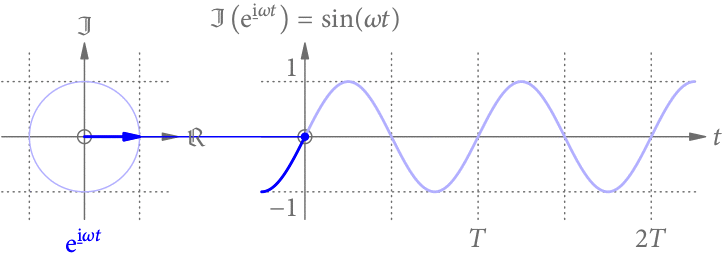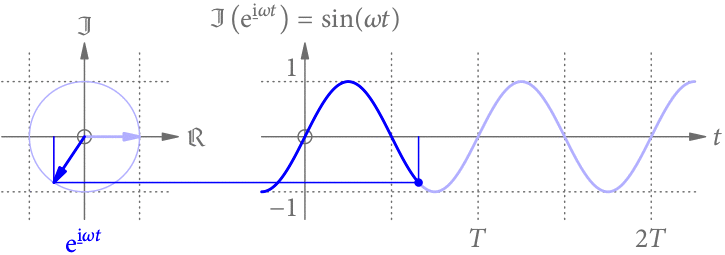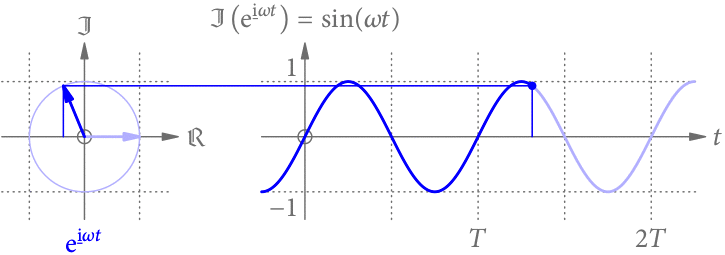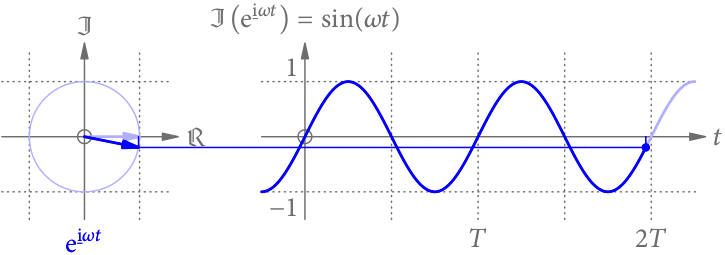
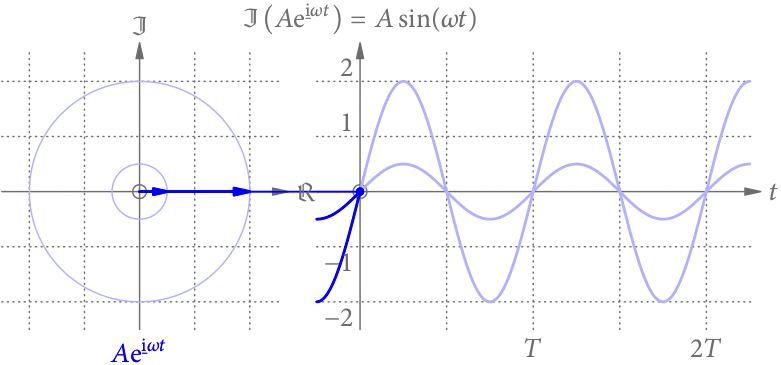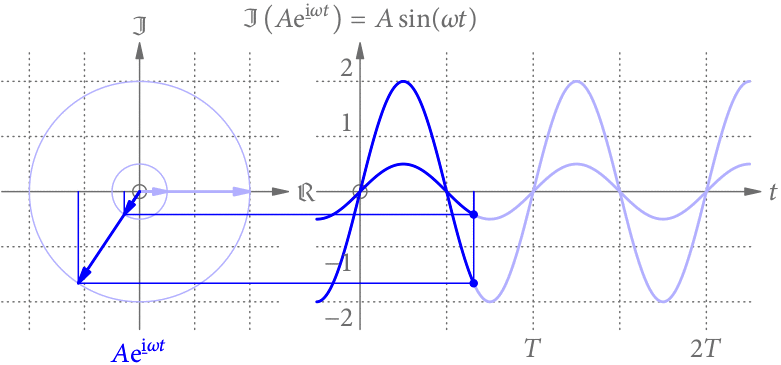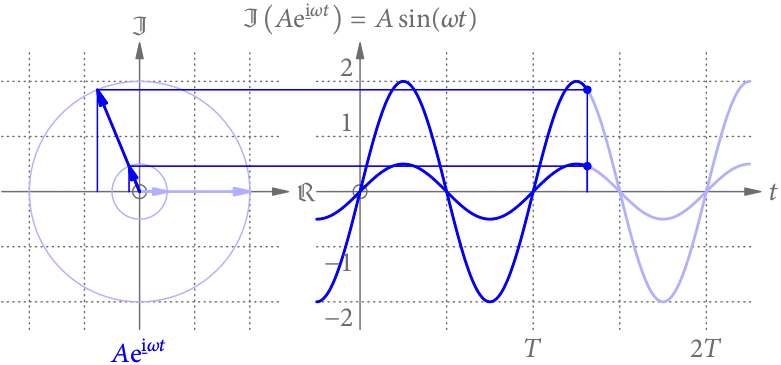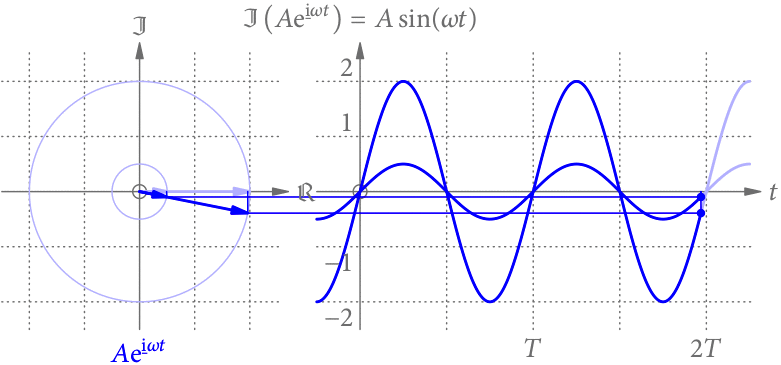
Die Sinus-Funktion

Projiziert man einen rotierenden Zeiger entlang der reellen Achse, sieht man nur seinen zeitlich veränderlichen Imaginärteil. Wenn der Zeiger zur Zeit t = 0 in Richtung der reellen Achse zeigt, definiert seine Zeitabhängigkeit die Sinus-Funktion (s. Abb. 2)

\displaystyle\Im\left(e^{\underline{i} \, \omega \, t}\right) = \sin(\omega \, t) .

Diese Funktion ist die Grundlage vieler Schwingungsvorgänge, und wird uns noch des Öfteren beschäftigen.

Abb. 2: Der Imaginärteil des gleichförmig rotierenden Zeigers e^{\underline{i} \, \omega \, t} als Funktion der Zeit ergibt die Sinus-Funktion \sin(\omega \, t).

Vergrößert (verkleinert) man die Frequenz, passen in dieselbe Zeit mehr (weniger) Perioden. Die Sinus-Funktion wird daher zeitlich gestaucht (gestreckt), wie in Abb. 3 gezeigt.

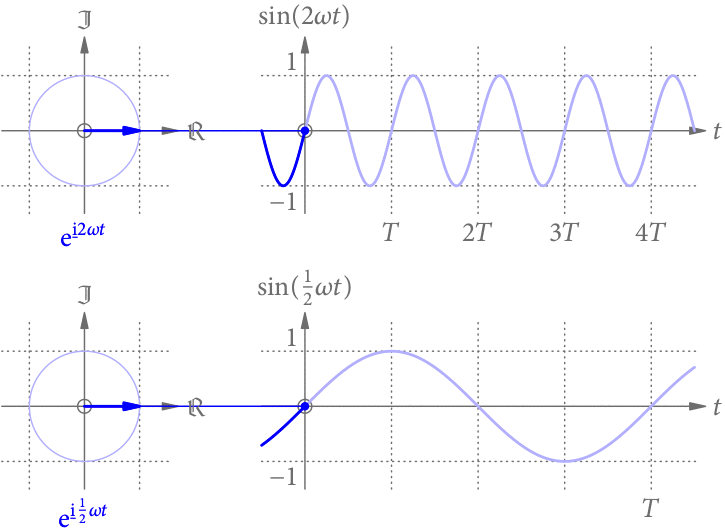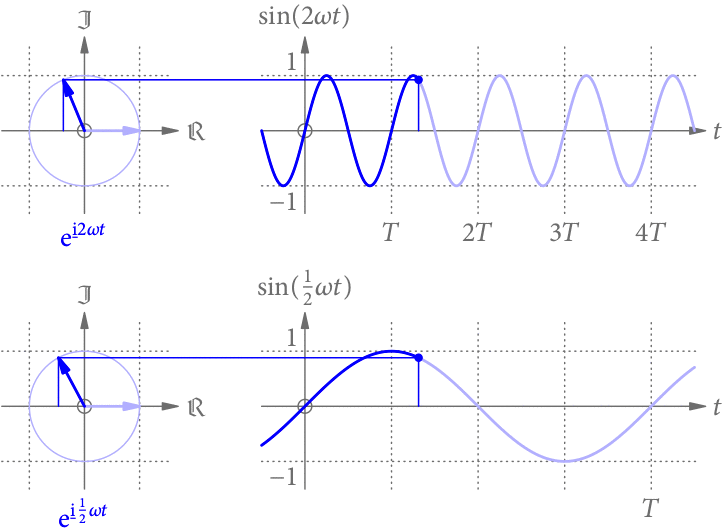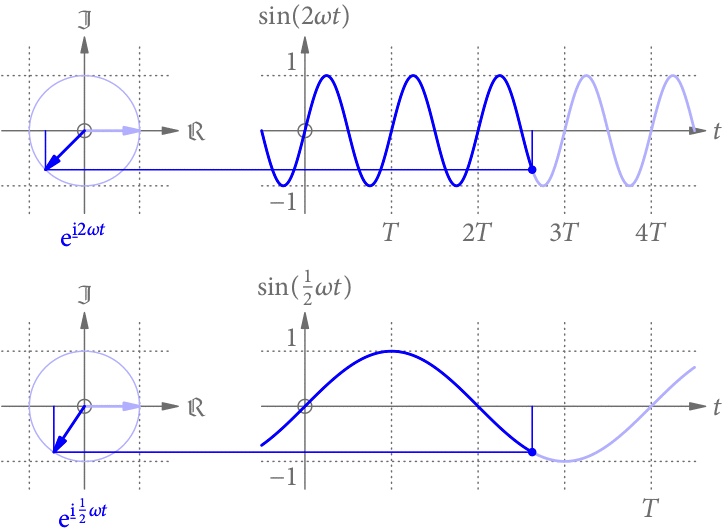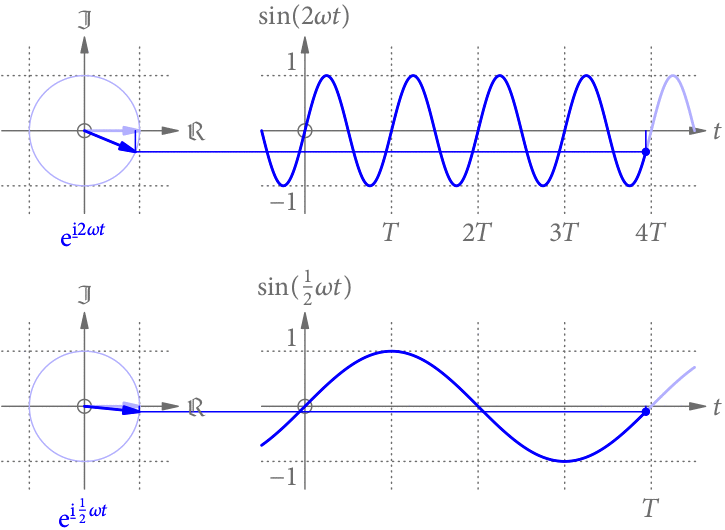
Abb. 3: Sinus-Funktionen mit der doppelten (oben) und der halben Frequenz (unten) wie in Abb. 2.

Amplitude und Phase

Multipliziert man den Zeiger e^{\underline{i} \, \omega \, t} mit einer positiven reellen Zahl A, wird der Zeiger länger (kürzer). Entsprechend wird die Sinus-Funktion in ihrer Höhe gestreckt (gestaucht), wie in Abb. 4 gezeigt. Man nennt diese Zahl die Amplitude A.

Abb. 4: Hat der Zeiger statt der Länge 1 die Länge A, wird die Sinus-Funktion in der Höhe gestreckt (A = 2) bzw. gestaucht (A = \frac{1}{2}).

Was, wenn der Zeiger zur Zeit 0 nicht in Richtung der reellen Achse zeigt, sondern den Winkel \varphi (die Phase) mit \Re hat? Nachdem der Zeiger einfach weiter im Kreis rotiert, ist die entstehende Funktion prinzipiell unverändert, aber in der Zeit verschoben (s. Abb. 5).

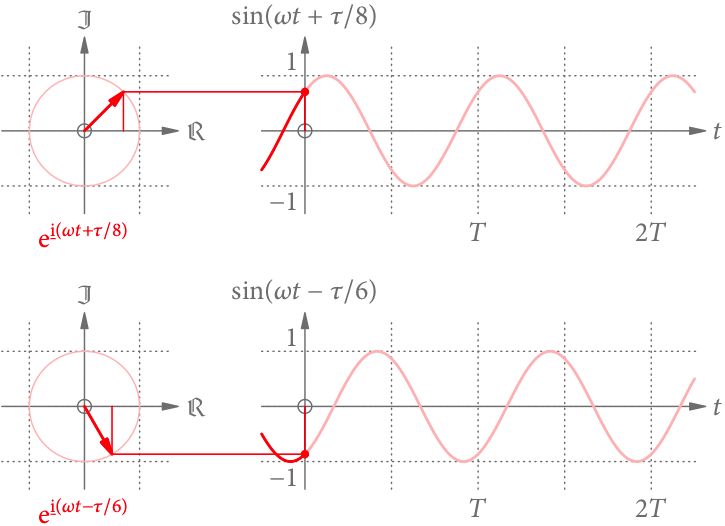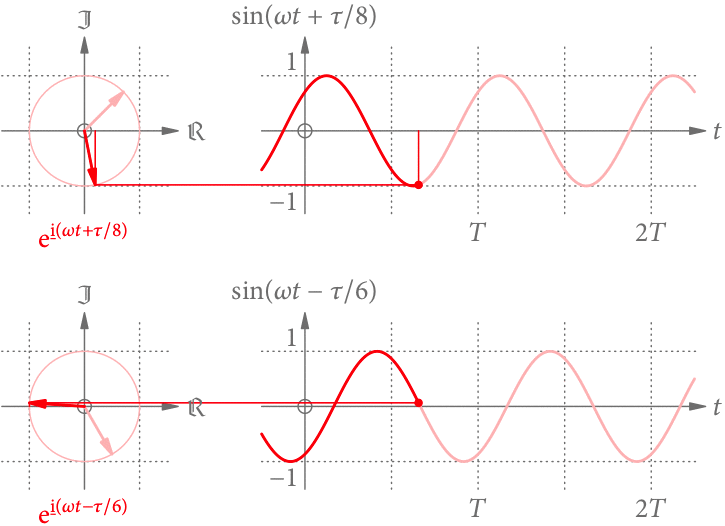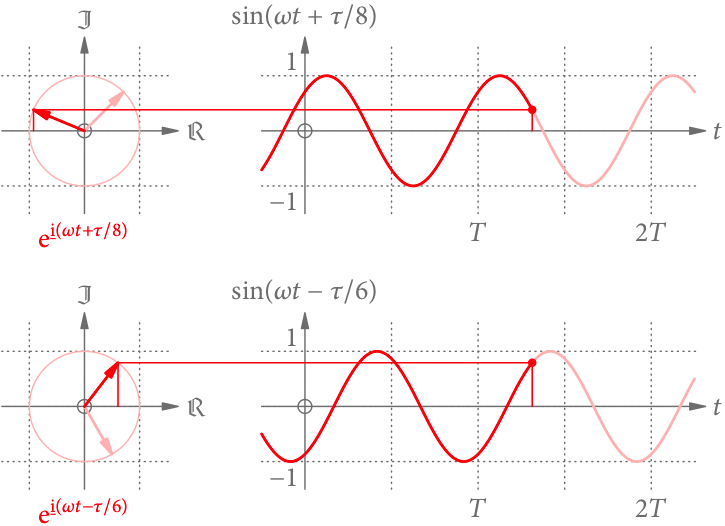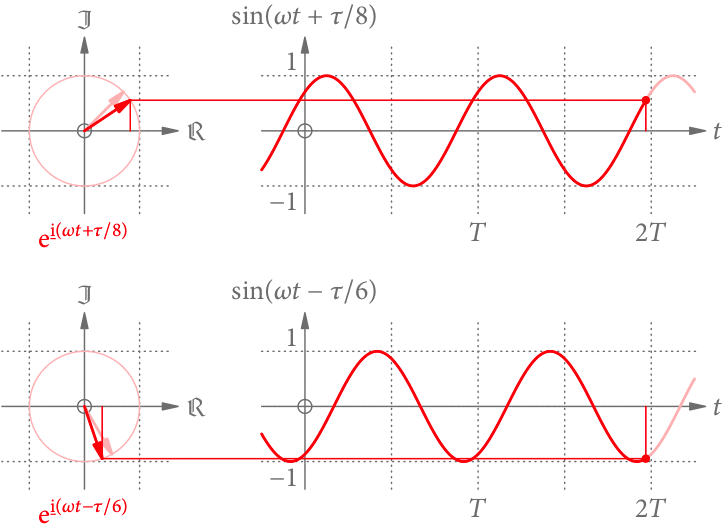
Abb. 5: Zu Beginn hat der Zeiger den Winkel \varphi = \tau/8 = 45^\circ (oben) bzw. \varphi = -\tau/6 = -60^\circ (unten) mit der reellen Achse. Die daraus resultierenden Sinus-Funktionen sind einfach nur zeitlich verschoben.

Die Phase \varphi verhält sich zum vollen Winkel \tau wie die zeitliche Verschiebung \Delta t zur Periodendauer T:

\displaystyle\frac{\varphi}{\tau} = -\frac{\Delta t}{T} .

Aber wo kommt das Minus her? Für \varphi > 0 (< 0) ist die Sinusfunktion zu früheren (späteren) Zeiten hin verschoben. Im ersten Fall ist der Zeiger nämlich früher bei einem bestimmten Winkel, im zweiten später.

Weil

A \, e^{\underline{i} \, (\omega \, t + \varphi)} = A \, e^{\underline{i} \, \varphi} \, e^{\underline{i} \, \omega \, t}

ist, können Amplitude und Phase zur komplexen Amplitude

\underline{A} = A \, e^{\underline{i} \, \varphi}

zusammengefasst werden. Diese ist ein Pfeil – manchmal auch Phasor genannt – und wird erst durch die Multiplikation mit e^{\underline{i} \, \omega \, t} zum rotierenden Zeiger.

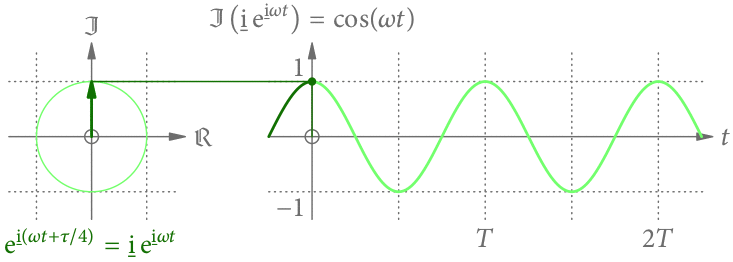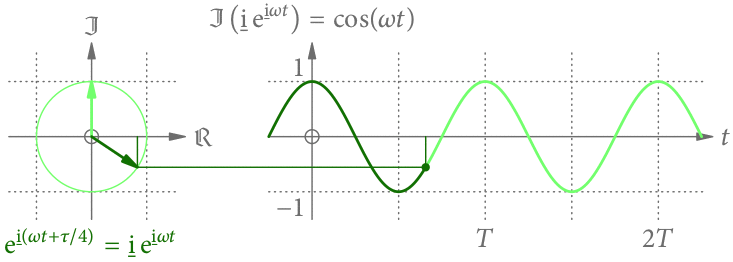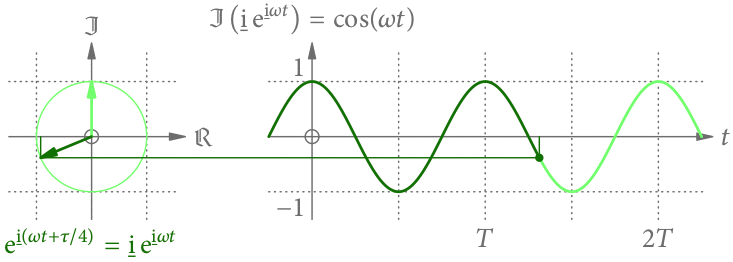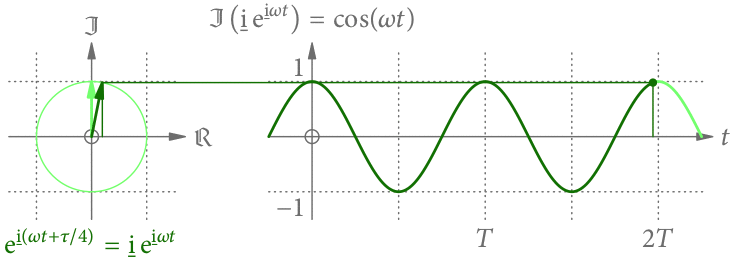
Die Cosinus-Funktion

Würde man statt dem Imaginär- den Realteil von e^{\underline{i} \, \omega \, t} nehmen, hätte man statt der Sinus- die Cosinus-Funktion bekommen. Es macht der Einheitlichkeit halber aber Sinn, immer nur den Imaginärteil zu nehmen. (Man hätte prinzipiell auch immer nur den Realteil nehmen können.)

Der Realteil wird aber durch Drehung um \tau/4 = 90^\circ zum Imaginärteil. Dieser Drehung entspricht genau eine Multiplikation mit der imaginären Einheit \underline{i} als komplexer Amplitude:

\Re\left(e^{\underline{i} \, \omega \, t}\right) = \Im\left(\underline{i} \, e^{\underline{i} \, \omega \, t}\right) = \Im\left(e^{\underline{i} \, (\omega t + \tau/4)}\right) = \sin(\omega \, t + \frac{\tau}{4}) = \cos(\omega \, t) .

Die Cosinus-Funktion entsteht also aus der Sinus-Funktion, wenn der Zeiger zur Zeit 0 in Richtung der imaginären Achse zeigt (s. Abb. 6).

Abb. 6: Die Cosinus-Funktion ergibt sich aus einem Zeiger, der zur Zeit t=0 entlang der imaginären Achse zeigt.

Mittelwert

Zuletzt stellt sich noch die Frage, warum unser Zeiger unbedingt um den Ursprung rotieren muss. Addiert man die komplexe Zahl \underline{m} zum Zeiger e^{\underline{i} \, \omega \, t}, kann man ihn um jeden beliebigen Punkt der Ebene rotieren lassen (s. Abb. 7).

Weil für die Projektion aber nur der Imaginärteil relevant ist, setzt man den Realteil von \underline{m} einfach immer gleich 0 und damit \underline{m} = m \, \underline{i}. Daher ist

\Im\left(e^{\underline{i} \, \omega \, t} + \underline{m}\right) = \Im\left(e^{\underline{i} \, \omega \, t} + m \, \underline{i}\right) =\Im\left(e^{\underline{i} \, \omega \, t}\right) + \Im\left(m \, \underline{i}\right) = \sin(\omega \, t) + m ,

weil Imaginärteil und Addition vertauschbar sind:

\Im(\underline{a} + \underline{b}) = \Im(\underline{a}) + \Im(\underline{b}) .

Abb. 7: Verschiebt man den Kreismittelpunkt entlang der imaginären Achse, verschiebt man ebenso die Sinus-Funktion nach oben (m > 0) bzw. nach unten (m < 0).

Die Spitze des Zeigers kann auf der imaginären Achse nie höher kommen als m + A und nie unter m - A. Man nennt m daher auch den Mittelwert (bzw. in der Elektrotechnik den Gleichanteil).

Summe zweier gleich schneller Zeiger

Bei Schwingungsphänomenen kommt es oft vor, dass man zwei Sinus-Funktionen gleicher Frequenz – aber unterschiedlicher Amplitude und Phase – addieren muss:

a \sin(\omega \, t + \varphi_1) + b \sin(\omega \, t + \varphi_2) .

Mit Zeigern können wir das schreiben als

\displaystyle\begin{aligned}\Im\left(a \, e^{\underline{i} \, \varphi_1} \, e^{\underline{i} \, \omega \, t}\right) + \Im\left(b \, e^{\underline{i} \, \varphi_2} \, e^{\underline{i} \, \omega \, t}\right) & = \Im\left[a \, e^{\underline{i} \, \varphi_1} \, e^{\underline{i} \, \omega \, t} + b \, e^{\underline{i} \, \varphi_2} \, e^{\underline{i} \, \omega \, t}\right] \\ &= \Im\left[\left(a \, e^{\underline{i} \, \varphi_1} + b \, e^{\underline{i} \, \varphi_2}\right) \cdot e^{\underline{i} \, \omega \, t}\right] \\ &= \Im\left(\underline{A} \, e^{\underline{i} \, \omega \, t}\right) \, ,\end{aligned}

wobei wir in der 2. Zeile e^{\underline{i} \, \omega \, t} herausgehoben haben. Am Ende erhalten wir also einen Pfeil, der mit derselben Geschwindigkeit rotiert, dessen komplexe Amplitude \underline{A} wir aber noch berechnen müssen. Die Summe zweier Sinus-Funktionen derselben Frequenz ergibt jedenfalls wieder eine Sinus-Funktion mit dieser Frequenz.

Abb. 8 demonstriert das anschaulich für den Spezialfall \varphi_1 = 0 und \varphi_2 = \tau/4. Die beiden Zeiger (blau und grün) rotieren mit derselben Geschwindigkeit, daher muss auch ihre Summe (rot) mit dieser Geschwindigkeit rotieren.

Abb. 8: Die Summe zweier Sinus-Funktionen gleicher Frequenz ist wieder eine Sinus-Funktion derselben Frequenz, aber i.Allg. mit unterschiedlicher Amplitude und Phase.

Für diesen Spezialfall können wir uns die Zeiger zur Zeit t = 0 in Abb. 9 ansehen (konkret: a = \sqrt{3} und b = 1). Blauer und grüner Pfeil bilden ein Rechteck und ihre rote Summe ist die Diagonale. Es folgt daher A = \sqrt{a^2+ b^2} = \sqrt{4} = 2 und \tan\varphi = b/a = 1/\sqrt{3}, d.h. \varphi = \tau/12 = 30^\circ.

Abb. 9: Die komplexen Amplituden für a \sin(\omega \, t) + b \cos(\omega \, t).

Für Schwingungen hat man daher den wichtigen Zusammenhang

a \cdot \sin(\omega t) + b \cdot \cos(\omega t) = A \cdot \sin(\omega t + \varphi)

mit

\displaystyle A = \sqrt{a^2 + b^2}    und    \displaystyle\tan(\varphi) = \frac{b}{a} .

Den allgemeinen Fall zur Zeit 0 zeigt Abb. 10: Aus dem Rechteck ist jetzt ein Parallelogramm geworden. Die Amplitude A ist die Länge der komplexen Amplitude \underline{A}, also A = \lvert\underline{A}\rvert = \sqrt{\underline{A} \cdot \underline{A}^*}, wobei der * das konjugiert Komplexe bedeutet:

\displaystyle\begin{aligned}A &= \sqrt{\left(a \, e^{\underline{i} \, \varphi_1} + b \, e^{\underline{i} \, \varphi_2}\right) \cdot \left(a \, e^{\underline{i} \, \varphi_1} + b \, e^{\underline{i} \, \varphi_2}\right)^*} \\ &= \sqrt{\left(a \, e^{\underline{i} \, \varphi_1} + b \, e^{\underline{i} \, \varphi_2}\right) \cdot \left(a \, e^{-\underline{i} \, \varphi_1} + b \, e^{-\underline{i} \, \varphi_2}\right)} \\ &= \sqrt{a^2 + ab\left[e^{\underline{i} \, (\varphi_1 - \varphi_2)} + e^{-\underline{i} \, (\varphi_1 - \varphi_2)}\right] + b^2} \, .\end{aligned}

Der Term in eckigen Klammern ist gemäß der Eulerschen Formel gleich 2 \cos(\varphi_1 - \varphi_2).

Abb. 10: Im allgemeinen Fall bilden die komplexen Amplituden ein Parallelogramm.

Für die resultierende Phase \varphi betrachten wir das große rechtwinkelige Dreieck in Abb. 10, dessen Hypotenuse gleich A ist. Die Ankathete an \varphi ist gleich a \cos(\varphi_1) + b \cos(\varphi_2) und die Gegenkathete ist gleich a \sin(\varphi_1) + b \sin(\varphi_2).

Für den allgemeinen Fall folgt daher

a \sin(\omega t + \varphi_1) + b \sin(\omega t + \varphi_2) = A \sin(\omega t + \varphi)

mit

A = \sqrt{a^2 + 2 ab \cos(\varphi_1 - \varphi_2) + b^2}

und

\displaystyle\tan(\varphi) = \frac{a \sin(\varphi_1) + b \sin(\varphi_2)}{a \cos(\varphi_1) + b \cos(\varphi_2)} .

Diskussion

Die allgemeine Sinus-Funktion aus einem rotierenden Zeiger zu generieren, hat in der Anwendung viele rechentechnische Vorteile: statt sich Unmengen trigonometrische Additionstheoreme auswendig zu merken, kann man einfach mit Exponentialfunktionen rechnen. Sehr häufig wird das in der Wechselstromtechnik getan.

Wir haben hier Sinus-Funktionen gleicher Frequenz addiert. In weiteren Beiträgen wird es dann um die Summe von Sinus-Funktionen mit unterschiedlichen Frequenzen gehen, was uns letztlich zur Fourier-Reihe und Fourier-Analyse führen wird. Methoden, die für die Signalanalyse und Signalverarbeitung von großer Bedeutung sind.

Weil wir die Zeiger in Richtung der reellen Achse projiziert haben, konnten wir einfach ihren Imaginärteil nehmen. Wir hätten genauso gut in jede andere Richtung projizieren können, wodurch sich aber nur die Phasen geändert hätten.

Ein Gedanke zu „Komplexe Zahlen, Teil 6 – rotierende Pfeile (Zeiger) und trigonometrische Funktionen“

Hinterlasse einen Kommentar

Diese Seite verwendet Akismet, um Spam zu reduzieren. Erfahre, wie deine Kommentardaten verarbeitet werden..