Komplexe Zahlen, Teil 2 – Multiplikation, Drehung und die Eulersche Formel

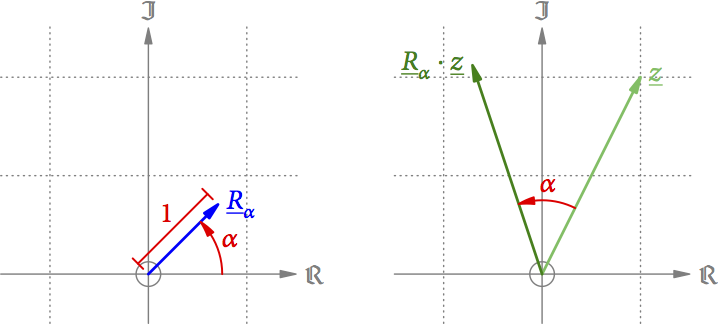
Im 1. Teil haben wir gesehen, dass die Multiplikation komplexer Zahlen eine Drehstreckung der entsprechenden Pfeile ist. Wie Abb. 1 zeigt, wird aus der Drehstreckung eine einfache Drehung, wenn einer der Pfeile die Länge 1 hat.

raz — Abb. 1: Der Pfeil $\underline{R}_\alpha$ hat die Länge 1 und den Winkel $\alpha$ zur positiven reellen Achse (links). Multipliziert man einen beliebigen Pfeil $\underline{z}$ mit $\underline{R}_\alpha$ , wird $\underline{z}$ einfach um den Winkel $\alpha$ gedreht (rechts).

Abb. 1: Der Pfeil $\underline{R}_\alpha$ hat die Länge 1 und den Winkel $\alpha$ zur positiven reellen Achse (links). Multipliziert man einen beliebigen Pfeil $\underline{z}$ mit $\underline{R}_\alpha$ , wird $\underline{z}$ einfach um den Winkel $\alpha$ gedreht (rechts).

Das haben wir schon bei der Multiplikation des Pfeils $\underline{i}$ mit sich selber gesehen, um $\underline{i}^2 = -1$ zu erhalten.

Dreht man $\underline{z}$ zuerst um den Winkel $\alpha$ und danach um den Winkel $\beta$ , hat man insgesamt um den Winkel $\alpha + \beta$ gedreht. Genauso gut hätte man zuerst um den Winkel $\beta$ und dann erst um den Winkel $\alpha$ drehen können. Die Vertauschbarkeit der Rotationen um die Winkel $\alpha$ und $\beta$ entspricht also der Kommutativität der Multiplikationen $\underline{R}_\alpha$ und $\underline{R}_\beta$ . Es muss daher gelten

$\underline{R}_\beta\cdot\underline{R}_\alpha=\underline{R}_\alpha\cdot\underline{R}_\beta=\underline{R}_{\alpha+\beta}$ .

Aus einer Multiplikation wird so eine Addition.

Beim Rechnen mit Potenzen hat man etwas Ähnliches. Aus einem Produkt wird die Summe der Exponenten

$a^n \cdot a^m = a^{n + m}$ .

Kann es also sein, dass $\underline{R}_\alpha$ eine Potenz

$\underline{R}_\alpha = (\underline{R}_1)^\alpha$

ist, wobei die Basis $\underline{R}_1$ ein noch zu bestimmender Pfeil ist?

Dabei ist $\underline{R}_1$ die Drehung um den Einheitswinkel. Das ist aber nicht 1°, weil die Teilung des vollen Winkels in 360° eine historische Willkür ist. Stattdessen verwendet man das Bogenmaß, bei dem der Einheitswinkel so gewählt wird, dass der entsprechende Kreisbogen ebenfalls die Länge 1 hat (s. Abb. 2). Umgerechnet ergibt das $\alpha = 1 \approx 57.3^\circ$ .

Abb. 2: Der Einheitswinkel $\alpha = 1 \approx 57.3^\circ$ ist so festgelegt, dass der entsprechende Kreisbogen die Länge 1 hat.

Abb. 2: Der Einheitswinkel $\alpha = 1 \approx 57.3^\circ$ ist so festgelegt, dass der entsprechende Kreisbogen die Länge 1 hat.

Aber welche komplexe Zahl ist $\underline{R}_1$ ? Dazu machen wir uns klar, dass die Drehung um den Einheitswinkel dasselbe ist, wie 2-mal hintereinander um den halben Einheitswinkel zu drehen. Oder 3-mal um ein Drittel des Einheitswinkels. Oder …

$\underline{R}_1 = (\underline{R}_{1/2})^2 = (\underline{R}_{1/3})^3 = \dotsb = (\underline{R}_{1/n})^n$ .

Was genau hat uns das jetzt gebracht? Nun, wenn $n$ sehr groß ist, dann ist $\underline{R}_{1/n}$ ein Pfeil der Länge 1, der den kleinen Winkel $1/n$ hat (s. Abb. 3).

r1n — Abb. 3: Der Realteil von $\underline{R}_{1/n}$ ist $\approx 1$ und der Imaginärteil ist $\approx 1/n$ .

In diesem Fall ist der Teil von $\underline{R}_{1/n}$ entlang der reellen Achse (der Realteil) $\approx 1$ und der Teil entlang der imaginären Achse (der Imaginärteil) ungefähr so lang wie der Kreisbogen $1/n$ . D.h.,

$\displaystyle\underline{R}_{1/n} \approx 1 + \frac{1}{n} \cdot \underline{i} = 1 + \frac{\underline{i}}{n}$ .

Daher ist für große $n$

$\displaystyle\underline{R}_1 = (\underline{R}_{1/n})^n \approx \left(1 + \frac{\underline{i}}{n}\right)^n$ .

In der reellen Analysis hat man so einen ähnlichen Ausdruck schon gesehen. Für große $n$ ist nämlich

$\displaystyle\left(1 + \frac{x}{n}\right)^n \approx e^x$ ,

wobei $e = 2.718\dots$ die Eulersche Zahl ist. Diese Näherung wird für $n \to \infty$ exakt.

Analog kann man daher vermuten, dass

$\displaystyle\underline{R}_1=e^{\underline{i}}$

ist. Die reelle Zahl $e=2.718\dots$ hoch die komplexe Zahl $\underline{i}$ , die mit sich selber multipliziert $\underline{i}^2 = -1$ ergibt, entspricht also einem Pfeil der Länge 1, der den Winkel $\alpha = 1 \approx 57.3^\circ$ zur positiven reellen Achse hat.

Damit erhält man weiter

$\displaystyle\underline{R}_\alpha=(\underline{R}_1)^\alpha=\left(e^{\underline{i}}\right)^\alpha=e^{\underline{i}\alpha}$ ,

wobei wir die Potenzrechenregel $(e^a)^b = e^{a \cdot b}$ verwendet haben. Der komplexen Zahl $e^{\underline{i}\alpha}$ entspricht also einfach ein Pfeil der Länge 1, der den beliebigen Winkel $\alpha$ zur positiven reellen Achse hat. Wenn man eine beliebige komplexe Zahl $\underline{z}$ hat, dreht eine Multiplikation mit $e^{\underline{i}\alpha}$ den entsprechenden Pfeil einfach um den Winkel $\alpha$ weiter.

Zeichnet man sich $\underline{R}_\alpha$ auf, kann man den Pfeil als Hypotenuse eines rechtwinkeligen Dreiecks sehen (s. Abb. 4). Der Realteil bildet die eine Kathete und kann als $\cos\alpha$ berechnet werden. Der Imaginärteil bildet die andere Kathete und ist gleich $\sin\alpha$ .

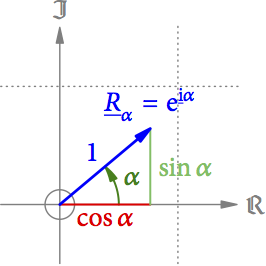
Daher muss

$\displaystyle\boxed{e^{\underline{i}\alpha} = \cos\alpha + \underline{i}\sin\alpha}$

sein. Das ist die berühmte Eulersche Formel.

Weiter in Teil 3.

Komplexe Zahlen, Teil 2 – Multiplikation, Drehung und die Eulersche Formel

Ähnliche Beiträge

Kommentar verfassen Antwort abbrechen